题目内容
已知,在△ABC中,∠C=90°,斜边长为7
,两直角边的长分别是关于x的方程x2-3(m+
)x+9m=0
的两个根,则△ABC的内切圆面积是( )
| 1 |
| 2 |
| 1 |
| 2 |
的两个根,则△ABC的内切圆面积是( )
| A、4π | ||
B、
| ||
C、
| ||
D、
|
分析:由根与系数的关系可得:x1+x2=3(m+
),x1•x2=9m;根据勾股定理得:x12+x22=(
)2,则整理得:m2-m-6=0,解关于m的一元二次方程可得m=3;又知直角三角形内切圆的半径r=
(a+b-c),则r=
,所以可求圆的面积为
π.
| 1 |
| 2 |
| 15 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
解答:解:∵x1+x2=3(m+
),x1•x2=9m;
∴x12+x22=(
)2,
整理得m2-m-6=0,
解得m=-2或3,
经验证m=-2不合题意,则m=3;
又∵直角三角形内切圆的半径r=
(a+b-c),
∴r=
,
∴圆的面积为
π.
| 1 |
| 2 |
∴x12+x22=(
| 15 |
| 2 |
整理得m2-m-6=0,
解得m=-2或3,
经验证m=-2不合题意,则m=3;
又∵直角三角形内切圆的半径r=
| 1 |
| 2 |
∴r=
| 3 |
| 2 |
∴圆的面积为
| 9 |
| 4 |
点评:本题考查了三角形的内切圆面积计算及根与系数的关系.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
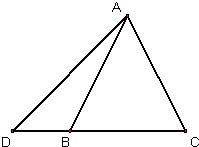 25、已知:在△ABC中AB=AC,点D在CB的延长线上.
25、已知:在△ABC中AB=AC,点D在CB的延长线上.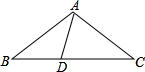 (1)化简:(a-
(1)化简:(a- 20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长.
20、如图,已知,在△ABC中,∠ABC和∠ACB的平分线交于点M,ME∥AB交BC于点E,MF∥AC交BC于点F.求证:△MEF的周长等于BC的长.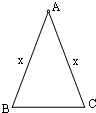 12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
12、已知,在△ABC中,AB=AC=x,BC=6,则腰长x的取值范围是
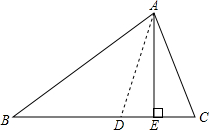 已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.
已知:在△ABC中,∠B<∠C,AD平分∠BAC,AE⊥BC,垂足为点E.∠B=38°,∠C=70°.