题目内容
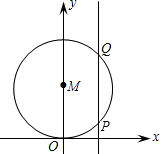 如图,⊙M与x轴相切于原点,平行于y轴的直线交圆于P、Q两点,P点在Q点的下方.若P点的坐标是(2,1),求圆心M的坐标.
如图,⊙M与x轴相切于原点,平行于y轴的直线交圆于P、Q两点,P点在Q点的下方.若P点的坐标是(2,1),求圆心M的坐标.
分析:过M作MN垂直于PQ,交PQ于N,根据垂径定理得到N为PQ中点,连接PM,由点P分别作x轴与y轴的垂线,交x轴于点A,与y轴交于点B,根据P的坐标得到PA和PB的长度,设圆心M的坐标为(0,m),则圆的半径MO=m,根据NA-PA表示出NP,而MN与PB相等,故在直角三角形MNP中,利用勾股定理列出关于m的方程,求出方程的解即可得到m的值,从而确定出圆心M的坐标.
解答: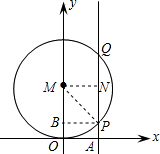 解:过M作MN⊥PQ,交PQ于N,连接PM,
解:过M作MN⊥PQ,交PQ于N,连接PM,
∴N为PQ的中点,
又P的坐标为(2,1),过P作PA⊥x轴,PB⊥y轴,
所以MN=PB=2,PA=1,
设圆心M的坐标为(0,m),由圆M与x轴相切于原点,
则圆的半径MP=m(m>0),NP=NA-PA=OM-PA=m-1,
在直角三角形MNP中,根据勾股定理得:
m2=(m-1)2+22,即2m=5,解得m=
,
则圆心M的坐标为(0,
).
 解:过M作MN⊥PQ,交PQ于N,连接PM,
解:过M作MN⊥PQ,交PQ于N,连接PM,∴N为PQ的中点,
又P的坐标为(2,1),过P作PA⊥x轴,PB⊥y轴,
所以MN=PB=2,PA=1,
设圆心M的坐标为(0,m),由圆M与x轴相切于原点,
则圆的半径MP=m(m>0),NP=NA-PA=OM-PA=m-1,
在直角三角形MNP中,根据勾股定理得:
m2=(m-1)2+22,即2m=5,解得m=
| 5 |
| 2 |
则圆心M的坐标为(0,
| 5 |
| 2 |
点评:本题考查了圆的切线性质,及解直角三角形的知识.在解决圆有关问题时,遇到圆中的弦,常常过圆心作这条弦的垂线,利用垂径定理得中点,由垂直构造以圆心、垂足及弦的一个端点为顶点的直角三角形解决有关问题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
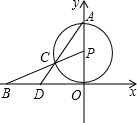 轴上.连接BP交⊙P于点C,连接AC并延长交x轴于点D.
轴上.连接BP交⊙P于点C,连接AC并延长交x轴于点D. 如图,⊙M与x轴相切于原点,平行于y轴的直线交⊙M于P、Q两点,P点在Q点的下方.若点P的坐标是(2,1),则圆心M的坐标是
如图,⊙M与x轴相切于原点,平行于y轴的直线交⊙M于P、Q两点,P点在Q点的下方.若点P的坐标是(2,1),则圆心M的坐标是 (2013•仓山区模拟)如图,⊙M与x轴相切与原点,平行于y轴的直线交⊙M于P、Q两点,P点在Q点的下方,若点P的坐标是
(2013•仓山区模拟)如图,⊙M与x轴相切与原点,平行于y轴的直线交⊙M于P、Q两点,P点在Q点的下方,若点P的坐标是 (2012•黔西南州模拟)如图,⊙P与x轴相切于坐标原点O,点A(0,2)是⊙P与y轴的交点,点B(
(2012•黔西南州模拟)如图,⊙P与x轴相切于坐标原点O,点A(0,2)是⊙P与y轴的交点,点B(