题目内容
如图，⊙M与x轴相切于原点，平行于y轴的直线交⊙M于P、Q两点，P点在Q点的下方．若点P的坐标是（2，1），则圆心M的坐标是（0，2.5）
（0，2.5）
．分析：先连接MP，过P作PA⊥y轴于A，再设M点的坐标是（0，b），且b＞0，由于PA⊥y轴，利用勾股定理易得AP2+AM2=MP2，即22+（b-1）2=b2，解即可．
解答：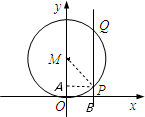
解：连接MP，过P作PA⊥y轴于A，
设M点的坐标是（0，b），且b＞0，
∵PA⊥y轴，
∴∠PAM=90°，
∴AP2+AM2=MP2，
∴22+（b-1）2=b2，
解得b=2.5，
故答案是（0，2.5）．
解：连接MP，过P作PA⊥y轴于A，设M点的坐标是（0，b），且b＞0，
∵PA⊥y轴，
∴∠PAM=90°，
∴AP2+AM2=MP2，
∴22+（b-1）2=b2，
解得b=2.5，
故答案是（0，2.5）．
点评：本题考查了切线的性质、勾股定理、坐标与图形性质．解题的关键是作辅助线，构造直角三角形，并知道MP=OM．
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
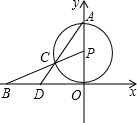轴上．连接BP交⊙P于点C，连接AC并延长交x轴于点D．
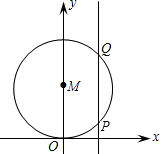如图，⊙M与x轴相切于原点，平行于y轴的直线交圆于P、Q两点，P点在Q点的下方．若P点的坐标是（2，1），求圆心M的坐标．
（2013•仓山区模拟）如图，⊙M与x轴相切与原点，平行于y轴的直线交⊙M于P、Q两点，P点在Q点的下方，若点P的坐标是
（2012•黔西南州模拟）如图，⊙P与x轴相切于坐标原点O，点A（0，2）是⊙P与y轴的交点，点B（