题目内容
 (2013•仓山区模拟)如图,⊙M与x轴相切与原点,平行于y轴的直线交⊙M于P、Q两点,P点在Q点的下方,若点P的坐标是(
(2013•仓山区模拟)如图,⊙M与x轴相切与原点,平行于y轴的直线交⊙M于P、Q两点,P点在Q点的下方,若点P的坐标是(| 2 |
| 2 |
| 2 |
(1)求⊙M的半径R;
(2)求图中阴影部分的面积(精确到0.1);
(3)已知直线AB对应的一次函数y=x+2+2
| 2 |
分析:(1)过M作MN⊥PQ于N,由垂径定理求出PN,求出NE,即可得出答案;
(2)连接MQ,MP,分别求出扇形QMP的面积和三角形QMP的面积,即可求出答案;
(3)过M作MT⊥AB于T,证△MTB∽△AOB,得出比例式,求出MT=2,即可得出答案.
(2)连接MQ,MP,分别求出扇形QMP的面积和三角形QMP的面积,即可求出答案;
(3)过M作MT⊥AB于T,证△MTB∽△AOB,得出比例式,求出MT=2,即可得出答案.
解答:解:(1)
过M作MN⊥PQ于N,
由垂径定理得:PN=QN=
PQ=
×2
=
,
∵点P的坐标是(
,2-
),
∴NE=2-
+
=2,
∵MN⊥PQ,MO⊥OE,PQ⊥OE,
∴∠MOE=∠OEN=∠MNP=90°,
∴四边形MOEN是矩形,
∴OM=NE=2,
即⊙M的半径是2;
(1)解:
y=x+2+2
,
当x=0时y=2+2
,
当y=0时,x=-2-2
,
即AO=OB=2+2
,
由勾股定理得:AB=2
+4,
连接MQ,MP,
在Rt△PNM中,PM=MO=2,PN=
,由勾股定理得:MN=
,
即MN=NP,
∵∠MNP=90°,
∴∠NMP=45°,
同理:∠QMN=45°,
∴∠QMP=90°,
∴阴影部分的面积S=S扇形QMP-S△QMP=
-
×2
×
=π-2;
(3)证明: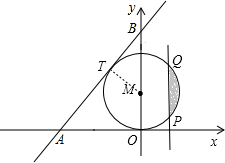
过M作MT⊥AB于T,
∵∠BOA=90°,
∴∠BTM=∠BOA,
∵∠ABO=∠MBT,
∴△BTM∽△BOA,
∴
=
,
∴
=
,
MT=2,
即MT⊥AB,MT为半径,
∴AB是⊙M的切线.

过M作MN⊥PQ于N,
由垂径定理得:PN=QN=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
∵点P的坐标是(
| 2 |
| 2 |
∴NE=2-
| 2 |
| 2 |
∵MN⊥PQ,MO⊥OE,PQ⊥OE,
∴∠MOE=∠OEN=∠MNP=90°,
∴四边形MOEN是矩形,
∴OM=NE=2,
即⊙M的半径是2;
(1)解:

y=x+2+2
| 2 |
当x=0时y=2+2
| 2 |
当y=0时,x=-2-2
| 2 |
即AO=OB=2+2
| 2 |
由勾股定理得:AB=2
| 2 |
连接MQ,MP,
在Rt△PNM中,PM=MO=2,PN=
| 2 |
| 2 |
即MN=NP,
∵∠MNP=90°,
∴∠NMP=45°,
同理:∠QMN=45°,
∴∠QMP=90°,
∴阴影部分的面积S=S扇形QMP-S△QMP=
| 90π•22 |
| 360 |
| 1 |
| 2 |
| 2 |
| 2 |
(3)证明:

过M作MT⊥AB于T,
∵∠BOA=90°,
∴∠BTM=∠BOA,
∵∠ABO=∠MBT,
∴△BTM∽△BOA,
∴
| BO |
| AB |
| OT |
| OA |
∴
2+2
| ||
2
|
| MT | ||
2+2
|
MT=2,
即MT⊥AB,MT为半径,
∴AB是⊙M的切线.
点评:本题考查了切线的性质和判定,相似三角形的性质和判定,扇形的面积,三角形的面积等知识点的应用,主要考查学生的推理和计算能力.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 (2013•仓山区模拟)如图,a∥b,∠1=30°,则∠2的度数是( )
(2013•仓山区模拟)如图,a∥b,∠1=30°,则∠2的度数是( ) (2013•仓山区模拟)如图,已知抛物线y=ax2+bx+c的顶点坐标是C(2,-1),与x轴交于点A(1,0),其对称轴与x轴相交于点F.
(2013•仓山区模拟)如图,已知抛物线y=ax2+bx+c的顶点坐标是C(2,-1),与x轴交于点A(1,0),其对称轴与x轴相交于点F.