题目内容
已知:如图,⊙P与x轴相切于坐标原点O,点A(0,2)是⊙P与y轴的交点,点B(-2| 2 |
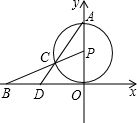 轴上.连接BP交⊙P于点C,连接AC并延长交x轴于点D.
轴上.连接BP交⊙P于点C,连接AC并延长交x轴于点D.(1)求线段BC的长;
(2)求直线AC的关系式;
(3)当点B在x轴上移动时,是否存在点B,使△BOP相似于△AOD?若存在,求出符合条件的点B的坐标;若不存在,请说明理由.
分析:(1)方法一:在直角三角形BOP中,根据勾股定理列方程求解;
方法二:延长BP交⊙P于G,根据切割线定理进行计算.
(2)要求直线AC的解析式,关键是求得点C的坐标.过点C作CE⊥x轴于E,CF⊥y轴于F,根据平行线分线段成比例定理求得CE、CF的长,再根据点C所在的象限写出它的坐标,从而根据待定系数法写出直线的解析式.
(3)要使△BOP相似于△AOD,因为∠OPB>∠OAD,所以∠OBP=∠OAD,结合圆周角定理,得∠OPB=2∠OBP,从而求得∠OBP=30°,则OB=cot30°•OP=
,即可写出点B的坐标,再根据对称性可以写出点B的另一种情况.
方法二:延长BP交⊙P于G,根据切割线定理进行计算.
(2)要求直线AC的解析式,关键是求得点C的坐标.过点C作CE⊥x轴于E,CF⊥y轴于F,根据平行线分线段成比例定理求得CE、CF的长,再根据点C所在的象限写出它的坐标,从而根据待定系数法写出直线的解析式.
(3)要使△BOP相似于△AOD,因为∠OPB>∠OAD,所以∠OBP=∠OAD,结合圆周角定理,得∠OPB=2∠OBP,从而求得∠OBP=30°,则OB=cot30°•OP=
| 3 |
解答: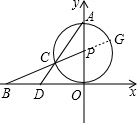 解:(1)
解:(1)
法一:由题意,得OP=1,BO=2
,CP=1.
在Rt△BOP中
∵BP2=OP2+BO2,
∴(BC+1)2=12+(2
)2,
∴BC=2.
法二:延长BP交⊙P于G,如图所示,由题意,得OB=2
,CG=2,
∵OB2=BC•BG,
∴(2
)2=BC•(BC+2),
BC=2.
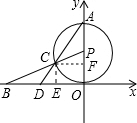 (2)如图所示,过点C作CE⊥x轴于E,CF⊥y轴于F.
(2)如图所示,过点C作CE⊥x轴于E,CF⊥y轴于F.
在△PBO中,
∵CF∥BO,
∴
=
.
即
=
,
解得CF=
.
同理可求得CE=
.
因此C(-
,
).
设直线AC的函数关系式为y=kx+b(k≠0).
把A(0,2),C(-
,
)两点代入关系式,得
,
解得
.
∴所求函数关系式为y=
x+2.
(3)如图所示,在x轴上存在点B,使△BOP与△AOD相似.
∵∠OPB>∠OAD,
∴∠OPB≠∠OAD.
故若要△BOP与△AOD相似,
则∠OBP=∠OAD.
又∠OPB=2∠OAD,
∴∠OPB=2∠OBP.
∵∠OPB+∠OBP=90°,
∴3∠OBP=90°,
∴∠OBP=30°.
因此OB=cot30°•OP=
.
∴B1点坐标为(-
,0).
根据对称性可求得符合条件的B2坐标(
,0).
综上,符合条件的B点坐标有两个:
B1(-
,0),B2(
,0).
 解:(1)
解:(1)法一:由题意,得OP=1,BO=2
| 2 |
在Rt△BOP中
∵BP2=OP2+BO2,
∴(BC+1)2=12+(2
| 2 |
∴BC=2.
法二:延长BP交⊙P于G,如图所示,由题意,得OB=2
| 2 |
∵OB2=BC•BG,
∴(2
| 2 |
BC=2.
 (2)如图所示,过点C作CE⊥x轴于E,CF⊥y轴于F.
(2)如图所示,过点C作CE⊥x轴于E,CF⊥y轴于F.在△PBO中,
∵CF∥BO,
∴
| CF |
| BO |
| PC |
| PB |
即
| CF | ||
2
|
| 1 |
| 3 |
解得CF=
2
| ||
| 3 |
同理可求得CE=
| 2 |
| 3 |
因此C(-
2
| ||
| 3 |
| 2 |
| 3 |
设直线AC的函数关系式为y=kx+b(k≠0).
把A(0,2),C(-
2
| ||
| 3 |
| 2 |
| 3 |
|
解得
|
∴所求函数关系式为y=
| 2 |
(3)如图所示,在x轴上存在点B,使△BOP与△AOD相似.
∵∠OPB>∠OAD,
∴∠OPB≠∠OAD.
故若要△BOP与△AOD相似,
则∠OBP=∠OAD.
又∠OPB=2∠OAD,
∴∠OPB=2∠OBP.
∵∠OPB+∠OBP=90°,
∴3∠OBP=90°,
∴∠OBP=30°.
因此OB=cot30°•OP=
| 3 |
∴B1点坐标为(-
| 3 |
根据对称性可求得符合条件的B2坐标(
| 3 |
综上,符合条件的B点坐标有两个:
B1(-
| 3 |
| 3 |
点评:此题综合运用了勾股定理、切割线定理、圆周角定理、平行线分线段成比例定理以及相似三角形的判定方法.要求能够熟练运用待定系数法求得函数的解析式.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
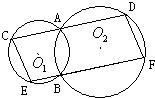 21、已知:如图,⊙O1与⊙O2相交于A、B两点,过A的直线交⊙O1于C,交⊙O2于D,过B的直线交⊙O1于E,交⊙O2于F,且CD∥EF.
21、已知:如图,⊙O1与⊙O2相交于A、B两点,过A的直线交⊙O1于C,交⊙O2于D,过B的直线交⊙O1于E,交⊙O2于F,且CD∥EF.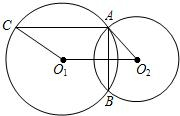 ,⊙O2的半径为
,⊙O2的半径为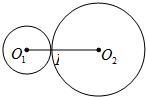 14、已知:如图,⊙O1与⊙O2外切于点P,⊙O1的半径为3,且O1O2=8,则⊙O2的半径R=
14、已知:如图,⊙O1与⊙O2外切于点P,⊙O1的半径为3,且O1O2=8,则⊙O2的半径R= (1997•南京)已知:如图,⊙O1与⊙O2外切于点P,A为⊙O1上一点,直线AC切⊙O2于点C,且交⊙O1于点B,AP的延长线交⊙O2于点D.
(1997•南京)已知:如图,⊙O1与⊙O2外切于点P,A为⊙O1上一点,直线AC切⊙O2于点C,且交⊙O1于点B,AP的延长线交⊙O2于点D.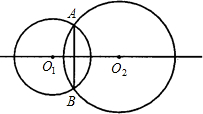 已知:如图,⊙O1与⊙O2相交于A,B两点.求证:直线O1O2垂直平分AB.
已知:如图,⊙O1与⊙O2相交于A,B两点.求证:直线O1O2垂直平分AB.