题目内容
【题目】如图，在四边形ABCD中，AD∥BC，∠B=90°，AD=8cm，AB=6cm，BC=10cm，点Q从点A出发以1cm/s的速度向点D运动，点P从点B出发以2cm/s的速度向C点运动，P、Q两点同时出发，其中一点到达终点时另一点也停止运动．若DP≠DQ，当t=_____s时，△DPQ是等腰三角形．
【答案】
或
．
【解析】
分两种情况讨论计算，求出时间，判断时间是否符合题意．
AQ=t,BP=2t,DQ=(8t)(cm),PC=(102t)(cm)，
∵△DPQ是等腰三角形，且DQ≠DP，
∴①当DP=QP时，∴点P在DQ的垂直平分线上，
∴
∴
∴
②当DQ=PQ时,如图,
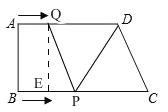
过点Q作QE⊥BC于E，
∴
∵AD∥BC，∠B=90°，
∴
，
∴四边形ABEQ是矩形，
∴EQ=AB=6，BE=AQ=t，
∴PE=BPBE=t，
在Rt△PEQ中,
∵DQ=8t
∴
∴
∵点P在边BC上，不和C重合，
∴
∴
∴此种情况符合题意，
即：
或时，△DPQ是等腰三角形。
故答案为：或．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
