题目内容
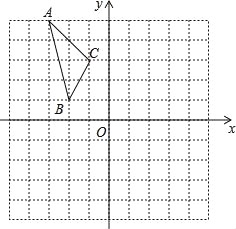
【题目】如图,四边形ABCD中,∠ABC=90°,AC=BD,AC⊥BD,若AB=4, AD=5,则DC的长 ( ).

A. 7 B. ![]() C.
C. ![]() D. 2
D. 2![]()
【答案】B
【解析】解:过D作DF⊥BA交BA的延长线于F.∵BE⊥AC,∴∠EBC+∠BCE=90°,∵∠ABC=90°,∴∠ABD+∠EBC=90°,∴∠ABE=∠BCA.在△BFD和△CBA中,∵∠ABE=∠BCA,∠F=∠ABC=90°,BD=CA,∴△BFD≌△CBA,∴DF=AB=4,BF=BC.在Rt△ADF中,∵AD=5,DF=4,∴AF=3,∴BC=3+4=7.∵∠DEC=90°,∴DC2=DE2+EC2=(BD-BE)2+EC2=(AC-BE)2+EC2
=AC2-2ACBE+BE2+EC2
= AC2-2ABBC+BC2
=![]()
=58
∴DC=![]() .
.


练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目