题目内容
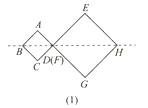
【题目】在长方形![]() 中,
中,![]() =
=![]() ,
,![]() =
=![]() ,点
,点![]() 从点
从点![]() 开始沿边
开始沿边![]() 向终点
向终点![]() 以
以![]() 的速度移动,与此同时,点
的速度移动,与此同时,点![]() 从点
从点![]() 开始沿边
开始沿边![]() 向终点
向终点![]() 以
以![]() 的速度移动.如果
的速度移动.如果![]() 、
、![]() 分别从
分别从![]() 、
、![]() 同时出发,当点
同时出发,当点![]() 运动到点
运动到点![]() 时,两点停止运动.设运动时间为
时,两点停止运动.设运动时间为![]() 秒.
秒.
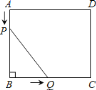
(1)填空:______=______,______=______(用含t的代数式表示);
(2)当![]() 为何值时,
为何值时,![]() 的长度等于
的长度等于![]() ?
?
(3)是否存在![]() 的面积等于
的面积等于![]() ?若存在,请求出此时
?若存在,请求出此时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() ;(2)当
;(2)当![]() =
=![]() 秒或
秒或![]() 秒时,
秒时,![]() 的长度等于
的长度等于![]() ;(3)存在
;(3)存在![]() =
=![]() 秒,能够使得五边形
秒,能够使得五边形![]() 的面积等于
的面积等于![]() .理由见解析.
.理由见解析.
【解析】
(1)根据点![]() 从点
从点![]() 开始沿边
开始沿边![]() 向终点
向终点![]() 以
以![]() 的速度移动,与此同时,点
的速度移动,与此同时,点![]() 从点
从点![]() 开始沿边
开始沿边![]() 向终点
向终点![]() 以
以![]() 的速度移动,可以求得
的速度移动,可以求得![]() ,
,![]() .
.
(2)用含t的代数式分别表示PB和BQ的值,运用勾股定理求得PQ为![]() =
=![]() 据此求出t值.
据此求出t值.
(3)根据题干信息使得五边形![]() 的面积等于
的面积等于![]() 的t值存在,利用长方形
的t值存在,利用长方形![]() 的面积减去
的面积减去![]() 的面积即可,有
的面积即可,有![]() 的面积为4,由此求得t值.
的面积为4,由此求得t值.
解:(1)点![]() 从点
从点![]() 开始沿边
开始沿边![]() 向终点
向终点![]() 以
以![]() 的速度移动,故
的速度移动,故![]() 为
为![]() ,点
,点![]() 从点
从点![]() 开始沿边
开始沿边![]() 向终点
向终点![]() 以
以![]() 的速度移动,
的速度移动,![]() =
=![]() ,故
,故![]() 为
为![]() .
.
(2)由题意得:![]() =
=![]() ,
,
解得:![]() =
=![]() ,
,![]() =
=![]() ;
;
当![]() =
=![]() 秒或
秒或![]() 秒时,
秒时,![]() 的长度等于
的长度等于![]() ;
;
(3)存在![]() =
=![]() 秒,能够使得五边形
秒,能够使得五边形![]() 的面积等于
的面积等于![]() .理由如下:
.理由如下:
长方形![]() 的面积是:
的面积是:![]() =
=![]() ,
,
使得五边形![]() 的面积等于
的面积等于![]() ,则
,则![]() 的面积为
的面积为![]() =
=![]() ,
,
![]() ,
,
解得:![]() =
=![]() (不合题意舍去),
(不合题意舍去),![]() =
=![]() .
.
即当![]() =
=![]() 秒时,使得五边形
秒时,使得五边形![]() 的面积等于
的面积等于![]() .
.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目