Question

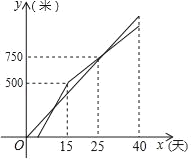
【题目】甲、乙两个工程队共同开凿一条隧道，甲队按一定的工作效率先施工，一段时间后，乙队从隧道的另一端按一定的工作效率加入施工，中途乙队调离一部分工人去完成其他任务，工作效率降低．当隧道气打通时，甲队工作了40天，设甲，乙两队各自开凿隧道的长度为y（米），甲队的工作时间为x（天），y与x之间的函数图象如图所示．

（1）求甲队的工作效率．

（2）求乙队调离一部分工人后y与x之间的函数关系式

（3）求这条隧道的总长度．

Answer 1

【答案】（1）30米/天；（2）y＝25x+125；（3）2325米；

【解析】

（1）根据函数图象中的数据可以求得甲的工作效率；

（2）根据函数图象中的数据可以求得乙队调离一部分工人后y与x之间的函数关系式；

（3）将x＝40代入（2）中的函数解析式可以求得乙开凿的隧道的长度，再根据甲的工作效率和工作时间可以求得甲开凿的隧道的长度，从而可以求得这条隧道的总长度．

解：（1）甲队的工作效率是：750÷25＝30米/天；

（2）设乙队调离一部分工人后y与x之间的函数关系式y＝kx+b，

，得，

即乙队调离一部分工人后y与x之间的函数关系式是y＝25x+125；

（3）将x＝40代入y＝25x+125，得

y＝25×40+125＝1125，

则这条隧道的总长度是：30×40+1125＝1200+1125＝2325（米），

答：这条隧道的总长度是2325米．