题目内容
【题目】已知抛物线C1:y=ax2+bx+c向左平移1个单位长度,再向上平移4个单位长度得到抛物线C2:y=x2.

(1)直接写出抛物线C1的解析式 ;
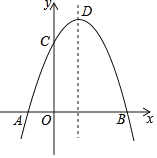
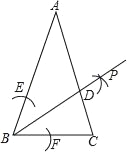
(2)如图1,已知抛物线C1与x轴交于A,B两点,点A在点B的左侧,点P(![]() ,t)在抛物线C1上,QB⊥PB交抛物线于点Q.求点Q的坐标;
,t)在抛物线C1上,QB⊥PB交抛物线于点Q.求点Q的坐标;
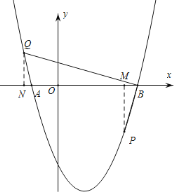
(3)已知点E,M在抛物线C2上,EM∥x轴,点E在点M的左侧,过点M的直线MD与抛物线C2只有一个公共点(MD与y轴不平行),直线DE与抛物线交于另一点N.若线段NE=DE,设点M,N的横坐标分别为m,n,直接写出m和n的数量关系(用含m的式子表示n)为 .
【答案】(1)y=(x﹣1)2﹣4;(2)Q(﹣![]() ,
,![]() );(3)n=(1±2
);(3)n=(1±2![]() )m
)m
【解析】
(1)逆向考虑,抛物线C2平移到抛物线C1,即可求抛物线C1的解析式;
(2)求出A、B、P的点的坐标,设Q(t,t2-2t-3),过点P作PM⊥x轴交于点M,过点Q作QN⊥x轴交于点N,可以证明△BNQ∽△QMP,由相似可得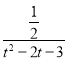 =
=![]() ,求出t即可;
,求出t即可;
(3)求出M、N、E点坐标,设MD的解析式为y=kx+b,将点M代入解析式可得y=kx+m2-km,再由直线MD与抛物线y=x2只有一个交点,联立方程kx+m2-km=x2,由判别式△=0可得k=2m,则直线MD为y=2mx-m2,在求出D点坐标代入MD的解析式即可求解.
(1)由已知可知,抛物线C2:y=x2向右平移1个单位长度,再向下平移4个单位长度得到抛物线C1:y=ax2+bx+c,
∴抛物线C1:y=(x﹣1)2﹣4,
故答案为y=(x﹣1)2﹣4;
(2)∵y=(x﹣1)2﹣4,
令y=0,(x﹣1)2﹣4=0,
解得x=3或x=﹣1,
∴A(﹣1,0),B(3,0),
∵点P(![]() ,t)在抛物线C1上,
,t)在抛物线C1上,
∴t=(![]() ﹣1)2﹣4,解得t=﹣
﹣1)2﹣4,解得t=﹣![]() ,
,
∴P(![]() ,﹣
,﹣![]() ),
),
设Q(t,t2﹣2t﹣3),
过点P作PM⊥x轴交于点M,过点Q作QN⊥x轴交于点N,
∵BQ⊥BP,
∴∠QBN+∠MBP=∠QBN+∠MQN=90°,
∴∠BQN=∠PBM,
∴△BNQ∽△QMP,
∴![]() =
=![]() ,
,
∴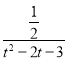 =
=![]() ,
,
∴t=﹣![]() 或t=3,
或t=3,
∵Q点在第二象限,
∴t=﹣![]() ,
,
∴Q(﹣![]() ,
,![]() );
);
(3)∵点M与N在y=x2上,
∴M(m,m2),N(n,n2)
∵EM∥x轴,
∴E(﹣m,m2),
设MD的解析式为y=kx+b,
∴m2=km+b,
∴b=m2﹣km,
∴y=kx+m2﹣km,
∵直线MD与抛物线y=x2只有一个交点,
∴kx+m2﹣km=x2,
∴△=k2﹣4(m2+km)=0,
∴k=2m,
∴直线MD的解析式为y=2mx﹣m2,
∵NE=DE,
∴D(﹣2m﹣n,2m2﹣n2),
∴2m2﹣n2=2m(﹣2m﹣n)﹣m2,
整理得,n2﹣2mn﹣7m2=0,
∴n=(1±2![]() )m,
)m,
故答案为n=(1±2![]() )m.
)m.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某公司共有![]() 三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.
三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.

各部门人数及每人所创年利润统计表
部门 | 员工人数 | 每人所创的年利润/万元 |
A | 5 | 10 |
B |
| 8 |
C |
| 5 |
(1)①在扇形图中,C部门所对应的圆心角的度数为___________;
②在统计表中,![]() ___________,
___________,![]() ___________;
___________;
(2)求这个公司平均每人所创年利润.