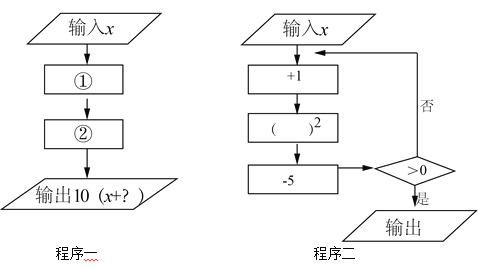
题目内容
【题目】已知:b是最大的负整数,且a,b,c满足|a+b|+(4-c)2016 =0,试回答问题:
(1)请直接写出a,b,c的值;
(2)若a,b,c所对应的点分别为A,B,C,点P为一动点,其对应的数为x,点P在0到1之间运动时(即0≤x≤1),请化简式子:|x+1|-|1-x|+2|x-4|;
(3)在(1)、(2)的条件下,点A,B,C开始在数轴上运动,若点A以每秒2个单位长度的速度向左运动,同时,点B和C分别以每秒3个单位长度和8个单位长度的速度向右运动,假设t秒后,若点B与点C之间的距离表示为BC,点A与B之间的距离表示为AB.请问:AB-BC的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
【答案】(1) a=-1,b=1,c=4;(2)8;(3) AB-BC的值是否随着时间t的变化而改变.
【解析】分析:(1)根据b是最大的负整数,即可得出b的值,再根据绝对值及偶次方的非负性即可得出a、c的值;(2)分析当0≤x≤1时,x+1、1-x、x-4的正负,去掉绝对值符号即可得出结论;(3)找出运动时间为t时,点A、B、C对应的数,再根据两点间的距离公式找出AB、BC的长度,二者做差后即可得出结论.
本题解析:
(1)∵b是最大的负整数,|a+b|+![]() =0,
=0,
∴b=1,a=b=1,c=4,
(2)∵0x1,
∴x+1>0,1x0,x4<0,
∴|x+1||1x|+2|x4|=x+1(1x)+2(4x)=8.
(3)ABBC的值随着时间t的变化而改变,理由如下:
运动时间为t时,点A对应的数为12t,点B对应的数为3t1,点C对应的数为8t+4,
∴AB=|12t(3t1)|=|5t2|,BC=|8t+4(3t1)|=|5t+5|,
∴ABBC=|5t2||5t5|.
当0t<![]() 时,ABBC=25t(55t)=3;
时,ABBC=25t(55t)=3;
当![]() t<1时,ABBC=5t2(55t)=10t7;
t<1时,ABBC=5t2(55t)=10t7;
当1t时,ABBC=5t2(5t5)=3.
综上所述:ABBC的值随着时间t的变化而改变。
点睛: 本题考查了有理数、绝对值和偶次方的非负性以及数轴,根据点的运动规则找出t秒后点对应的数是解题的关键.

【题目】某班第一组12名同学在“爱心捐款”活动中,捐款情况统计如下表,则捐款数组成的一组数据中,中位数与众数分别是( )
捐款(元) | 10 | 15 | 20 | 50 |
人数 | 1 | 5 | 4 | 2 |
A.15,15
B.17.5,15
C.20,20
D.15,20