题目内容
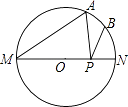
【题目】如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE.若DE:AC=3:5,则 ![]() 的值为( )
的值为( ) 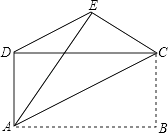
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:∵矩形沿直线AC折叠,点B落在点E处,
∴∠BAC=∠EAC,AE=AB=CD,
∵矩形ABCD的对边AB∥CD,
∴∠DCA=∠BAC,
∴∠EAC=∠DCA,
设AE与CD相交于F,则AF=CF,
∴AE﹣AF=CD﹣CF,
即DF=EF,
∴ ![]() =
= ![]() ,
,
又∵∠AFC=∠EFD,
∴△ACF∽△EDF,
∴ ![]() =
= ![]() =
= ![]() ,
,
设DF=3x,FC=5x,则AF=5x,
在Rt△ADF中,AD= ![]() =
= ![]() =4x,
=4x,
又∵AB=CD=DF+FC=3x+5x=8x,
∴ ![]() =
= ![]() =
= ![]() .
.
故选A.
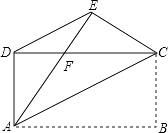
首先设AE与CD相交于F,根据折叠的性质可得△ACF、△DEF是等腰三角形,继而证得△ACF∽△EDF,然后由相似三角形的对应边成比例,求得DF:FC=3:5,再设DF=3x,FC=5x,即可求得AB,继而求得答案.

练习册系列答案
相关题目