题目内容
.已知如图,正方形AEDG的两个顶点A、D都在⊙O上,AB为⊙O直径,射线线ED与⊙O的另一个交点为C,试判断线段AC与线段BC的关系.
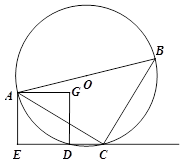

解:线段AC与线段BC垂直且相等 ………1分

证明:连结AD ………2分
∵四边形AEDG为正方形
∴∠ADE=45°
∵四边形ABCD内接⊙O
∴∠B+∠ADC=180° ……...3分
又∵∠ADE+∠ADC=180°
∴∠B=∠ADE=45°
又∵AB为⊙O直径
∴∠ACB=90°,即AC⊥BC ……4分
∴∠BAC=45°
∴AC=BC ……..5分

证明:连结AD ………2分
∵四边形AEDG为正方形
∴∠ADE=45°
∵四边形ABCD内接⊙O
∴∠B+∠ADC=180° ……...3分
又∵∠ADE+∠ADC=180°
∴∠B=∠ADE=45°
又∵AB为⊙O直径
∴∠ACB=90°,即AC⊥BC ……4分
∴∠BAC=45°
∴AC=BC ……..5分
略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

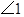 的正切值等于
的正切值等于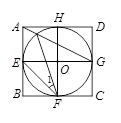
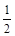
 中,
中,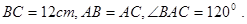

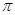 ?
?