题目内容
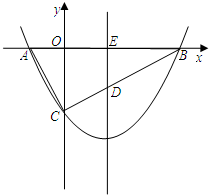 如图,Rt△ABC中,斜边AB在x轴上,C点在y轴上,A点坐标为(-2,0),B点坐标为(8,0),
如图,Rt△ABC中,斜边AB在x轴上,C点在y轴上,A点坐标为(-2,0),B点坐标为(8,0),(1)直接写出点C的坐标:
(0,-4)
(0,-4)
,并求出经过点A、B、C的抛物线解析式.(2)若抛物线的对称轴DE交BC于D,在对称轴上存在点P,使得以C、D、P为顶点的三角形与△ABC相似,请直接写出点P的坐标:
(3,-4)或(3,-10)
(3,-4)或(3,-10)
.(3)在抛物线的BC段上有一动点M,当M在什么位置时,△BCM的面积最大?并求此时△BCM的面积.
分析:(1)易得△AOC∽△COB,根据对应边成比例可求出OC,继而得出点C的坐标,利用待定系数法求出抛物线解析式即可;
(2)分两种情况讨论,①∠CPD=90°,②∠PCD=90°,确定点P的纵坐标,即可得出答案.
(3)在抛物线的BC段上取点M,连接MC,MB,作MN⊥AB交BC于N,设点M的坐标为(x,
(x-8)(x-2)),求出直线BC的解析式,可表示出点N的坐标,继而得出MN的长度,再由△BCM的面积=
MN×OB,可得出S△BCM关于x的表达式,利用配方法求最值即可.
(2)分两种情况讨论,①∠CPD=90°,②∠PCD=90°,确定点P的纵坐标,即可得出答案.
(3)在抛物线的BC段上取点M,连接MC,MB,作MN⊥AB交BC于N,设点M的坐标为(x,
| 1 |
| 4 |
| 1 |
| 2 |
解答:解:(1)∵∠ACO+∠BCO=90°,∠OBC+∠BCO=90°,
∴∠ACO=∠OBC,
又∵∠AOC=∠COB=90°,
∴△AOC∽△COB,
∴
=
,即
=
,
∴OC=4,
故点C的坐标为:(0,-4);
依题意可设经过点A、B、C的抛物线解析式为:y=a(x-8)(x+2),
将C的坐标:(0,-4)代入得-4=a(0-8)(0+2),
解得:a=
,
故过点A、B、C的抛物线解析式为:y=
(x-8)(x+2).
(2)设直线BC的解析式为y=kx+b,
将B、C的坐标代入得:
,
解得:
,
故直线BC的解析式为:y=
x-4,
抛物线解析式为y=
(x-8)(x+2)=
(x-3)2-
,
则抛物线的对称轴为:x=3,
∴点D的坐标为(3,-
),
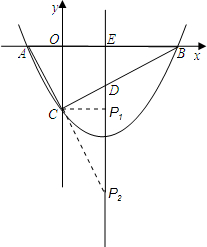
①若∠CPD=90°,
此时∠CDP1=∠BDE=∠BAC,
∴△ABC∽△DCP1,
∴
=
,即
=
,
解得:DP1=
,
故P1的坐标为(3,-4);
若∠PCD=90°,此时∠P2DC=∠BDE=∠BAC,
∴△ABC∽△DP2C,
∴∠CP2P1=∠ABC,
∴△CP2P1∽△COB,
∴
=
,即
=
,
解得:P1P2=6,
故P2的坐标为:(3,-10);
综上可得:点P的坐标为:(3,-4)或(3,-10).
(3)在抛物线的BC段上取点M,(如图)连接MC,MB,作MN⊥AB交BC于N,
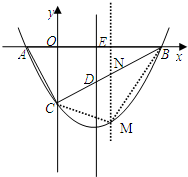
设M的坐标为(x,
(x-8)(x-2)),N的坐标为(x,
x-4),
则MN=
x-4-
(x-8)(x+2)=-
x2+2x,
∴S△BCM=
MN×OB=-x2+8x=-(x-4)2+16,
∵a=-1<0,
∴当x=4时,△BCM的面积最大,最大为16.
此时M的坐标为(4,-6).
∴∠ACO=∠OBC,
又∵∠AOC=∠COB=90°,
∴△AOC∽△COB,
∴
| AO |
| CO |
| CO |
| OB |
| 2 |
| OC |
| OC |
| 8 |
∴OC=4,
故点C的坐标为:(0,-4);
依题意可设经过点A、B、C的抛物线解析式为:y=a(x-8)(x+2),
将C的坐标:(0,-4)代入得-4=a(0-8)(0+2),
解得:a=
| 1 |
| 4 |
故过点A、B、C的抛物线解析式为:y=
| 1 |
| 4 |
(2)设直线BC的解析式为y=kx+b,
将B、C的坐标代入得:
|
解得:
|
故直线BC的解析式为:y=
| 1 |
| 2 |
抛物线解析式为y=
| 1 |
| 4 |
| 1 |
| 4 |
| 25 |
| 4 |
则抛物线的对称轴为:x=3,
∴点D的坐标为(3,-
| 5 |
| 2 |

①若∠CPD=90°,
此时∠CDP1=∠BDE=∠BAC,
∴△ABC∽△DCP1,
∴
| DP1 |
| AC |
| CP1 |
| BC |
| DP1 | ||
2
|
| 3 | ||
4
|
解得:DP1=
| 3 |
| 2 |
故P1的坐标为(3,-4);
若∠PCD=90°,此时∠P2DC=∠BDE=∠BAC,
∴△ABC∽△DP2C,
∴∠CP2P1=∠ABC,
∴△CP2P1∽△COB,
∴
| CP1 |
| OC |
| P1P2 |
| OB |
| 3 |
| 4 |
| P1P2 |
| 8 |
解得:P1P2=6,
故P2的坐标为:(3,-10);
综上可得:点P的坐标为:(3,-4)或(3,-10).
(3)在抛物线的BC段上取点M,(如图)连接MC,MB,作MN⊥AB交BC于N,

设M的坐标为(x,
| 1 |
| 4 |
| 1 |
| 2 |
则MN=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
∴S△BCM=
| 1 |
| 2 |
∵a=-1<0,
∴当x=4时,△BCM的面积最大,最大为16.
此时M的坐标为(4,-6).
点评:本题考查了二次函数的综合,涉及了待定系数法求函数解析式、相似三角形的判定与性质及配方法求最值的知识,综合性较强,解答本题需要具有扎实的基本功,将所学知识融会贯通,注意分类讨论思想及数形结合思想的运用.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目

 如图,Rt△ABC中,∠ACB=90°,tanB=
如图,Rt△ABC中,∠ACB=90°,tanB= 如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( )
如图,Rt△ABC中,∠C=90°,BC=3,AC=4,若△ABC∽△BDC,则CD=( ) 如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F.
如图,Rt△ABC中,∠C=90°,△ABC的内切圆⊙0与BC、CA、AB分别切于点D、E、F. 如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.
如图,Rt△ABC中,∠ABC=90゜,BD⊥AC于D,∠CBD=α,AB=3,BC=4.