Question

【题目】如图，以M（﹣5，0）为圆心、4为半径的圆与x轴交于A、B两点，P是⊙M上异于A、B的一动点，直线PA、PB分别交y轴于C、D，以CD为直径的⊙N与x轴交于E、F，则EF的长（ ）
A.等于4
B.等于4
C.等于6
D.随P点位置的变化而变化

Answer 1

【答案】C
【解析】解：连接NE， 设圆N半径为r，ON=x，则OD=r﹣x，OC=r+x，
∵以M（﹣5，0）为圆心、4为半径的圆与x轴交于A、B两点，
∴OA=4+5=9，0B=5﹣4=1，
∵AB是⊙M的直径，
∴∠APB=90°（直径所对的圆周角是直角），
∵∠BOD=90°，
∴∠PAB+∠PBA=90°，∠ODB+∠OBD=90°，
∵∠PBA=∠OBD，
∴∠PAB=∠ODB，
∵∠APB=∠BOD=90°，
∴△OBD∽△OCA，
∴ ，
即 = ，
（r+x）（r﹣x）=9，
r2﹣x2=9，
由垂径定理得：OE=OF，OE2=EN2﹣ON2=r2﹣x2=9，
即OE=OF=3，
∴EF=2OE=6，
故选：C．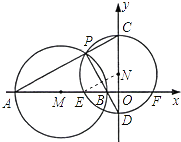

【考点精析】本题主要考查了勾股定理的概念和垂径定理的相关知识点，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧才能正确解答此题．