题目内容
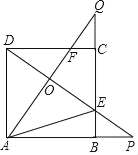
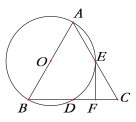
【题目】如图，在
以AB为直径的圆交AC、BC与点E和点D，AB=6，且E为AC的中点，过E点作
（1）求
的值
（2）连接OF并求OF的长
【答案】（1）
；（2）OF=
.
【解析】
（1）连接BE，证明△ABC为等边三角形，求出BC和EF的值即可得出结论；
（2）连接OF，过点O作OM⊥BC，分别求出OM，MF的长，再由勾股定理即可得出结论.
(1)连接BE，
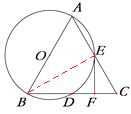
∵AB为圆O的直径，
∴BE⊥AC
又∵E为AC的中点
∴AB=BC
∵AC=BC
∴AB=BC=AC=6
即△ABC为等边三角形
∴∠ABC=∠C=60°
∴EF=CEsin60°=
∴；
(2) 连接OF，过点O作OM⊥BC，如图，
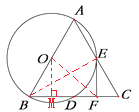
则
BM=
OB=
AB=
，CF=CE=AC=，
∴OM = OB*sin60°=ABsin60°=
∴MF=BC - BM - CF=6--=3
∴OF=
.
练习册系列答案
阅读快车系列答案
相关题目
【题目】在同样条件下对某种小麦种子进行发芽试验，统计发芽种子数，获得如下频数表．
试验种子n（粒） | 1 | 5 | 50 | 100 | 200 | 500 | 1000 | 2000 | 3000 |
发芽频数m | 1 | 4 | 45 | 92 | 188 | 476 | 951 | 1900 | 2850 |
发芽频率 | 0 | 0.80 | 0.90 | 0.92 | 0.94 | 0.952 | 0.951 | a | b |
（1）计算表中a，b的值；
（2）估计该麦种的发芽概率；
（3）如果该麦种发芽后，只有87%的麦芽可以成活，现有100kg麦种，则有多少千克的麦种可以成活为秧苗？
