Question

已知一次函数y=2x+b和y=-x+a的图象都经过A（0，-4），且与x轴分别交于B，C两点，则△ABC的面积应为（　　）

• A、13
• B、14
• C、11
• D、12

Answer 1

分析：把A（0，-4）分别代入一次函数y=2x+b和y=-x+a中求出a和b值，进而确定B，C两点的坐标，方可求出△ABC的面积．

解答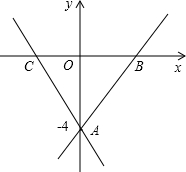：解：把A（0，-4）分别代入一次函数y=2x+b和y=-x+a
得：b=-4，a=-4，当y=0时两直线与x轴相交，
2x-4=0，x=2；
-x-4=0，x=-4；
故B，C两点的坐标分别为B（2，0），C（-4，0），则BC=|-4-2|=6，
OA=|-4|=4，则△ABC的面积应为

1

2

×BC×OA=

1

2

×6×4=12．
故选D．

点评：本题要注意利用一次函数的特点，列出方程，求出未知数，再求出三角形的底边长和高，从而求得其面积．