题目内容
【题目】在矩形ABCD中,E为CD的中点,H为BE上的一点, ![]() ,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.
,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F. 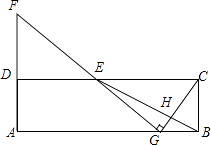
(1)求证: ![]() ;
;
(2)若∠CGF=90°,求 ![]() 的值.
的值.
【答案】
(1)证明:∵四边形ABCD是矩形,
∴CD∥AB,AD=BC,AB=CD,AD∥BC,
∴△CEH∽△GBH,
∴ ![]()
(2)解:作EM⊥AB于M,如图所示:
则EM=BC=AD,AM=DE,
∵E为CD的中点,
∴DE=CE,
设DE=CE=3a,则AB=CD=6a,
由(1)得: ![]() =3,
=3,
∴BG= ![]() CE=a,
CE=a,
∴AG=5a,
∵∠EDF=90°=∠CGF,∠DEF=∠GEC,
∴△DEF∽△GEC,
∴ ![]() ,
,
∴EGEF=DEEC,
∵CD∥AB,
∴ ![]() =
= ![]() ,
,
∴ ![]() ,
,
∴EF= ![]() EG,
EG,
∴EG ![]() EG=3a3a,
EG=3a3a,
解得:EG= ![]() a,
a,
在Rt△EMG中,GM=2a,
∴EM= ![]() =
= ![]() a,
a,
∴BC= ![]() a,
a,
∴ ![]() =
= ![]() =3
=3 ![]() .
.

【解析】(1)根据相似三角形判定的方法,判断出△CEH∽△GBH,即可推得 ![]() .(2)作EM⊥AB于M,则EM=BC=AD,AM=DE,设DE=CE=3a,则AB=CD=6a,由(1)得:
.(2)作EM⊥AB于M,则EM=BC=AD,AM=DE,设DE=CE=3a,则AB=CD=6a,由(1)得: ![]() =3,得出BG=
=3,得出BG= ![]() CE=a,AG=5a,证明△DEF∽△GEC,由相似三角形的性质得出EGEF=DEEC,由平行线证出
CE=a,AG=5a,证明△DEF∽△GEC,由相似三角形的性质得出EGEF=DEEC,由平行线证出 ![]() ,得出EF=
,得出EF= ![]() EG,求出EG=
EG,求出EG= ![]() a,在Rt△EMG中,GM=2a,由勾股定理求出BC=EM=
a,在Rt△EMG中,GM=2a,由勾股定理求出BC=EM= ![]() a,即可得出结果.此题主要考查了相似三角形的判定与性质、矩形的性质勾股定理等知识;熟练掌握矩形的性质,证明三角形相似是解决问题的关键.
a,即可得出结果.此题主要考查了相似三角形的判定与性质、矩形的性质勾股定理等知识;熟练掌握矩形的性质,证明三角形相似是解决问题的关键.
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案