题目内容
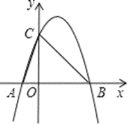
【题目】如图,抛物线y=﹣x2+2x+3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.将抛物线沿y轴平移t(t>0)个单位,当平移后的抛物线与线段OB有且只有一个交点时,则t的取值范围是___.
【答案】![]() 或
或![]()
【解析】
把函数y=﹣x2+2x+3化为顶点式y=a(x-h)2+k,向下平移使抛物线与线段OB有且只有一个交点,需找到临界值以及单独分析顶点落在x轴的情况.
解:分析题意可知,抛物线只能沿y轴向下平移,
∵y=-x2+2x+3=-(x-1)2+4,
∴平移后的抛物线的解析式为y=-(x-1)2+4-t(t>0),
当抛物线过原点时,抛物线与线段OB有两个交点,
此时,把(0,0)代入得:0=-(0-1)2+4-t,
解得t=3;
当平移后的抛物线的顶点落在x轴上时,x=1,y=0,
代入解析式得:0=-(1-1)2+4-t,
解得t=4,
若使平移后的抛物线与线段OB有且只有一个交点,
则0<t<3或t=4,
故答案为:0<t<3或t=4.

练习册系列答案
相关题目
【题目】在水果销售旺季,某水果店购进一优质水果,进价为20元/千克,售价不低于20元/千克,且不超过32元/千克,根据销售情况,发现该水果一天的销售量y(千克)与该天的售价x(元/千克)满足如下表所示的一次函数关系.
销售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为23.5元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利150元,那么该天水果的售价为多少元?