题目内容
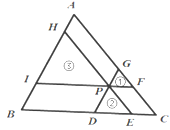
【题目】如图,过![]() 内一点分别作三边的平行线,形成三个小三角形①、②、③,如果这三个小三角形面积分别为1、4、9,则
内一点分别作三边的平行线,形成三个小三角形①、②、③,如果这三个小三角形面积分别为1、4、9,则![]() 的面积为____________
的面积为____________
 .
.
【答案】36
【解析】
由过△ABC内一点分别作三边的平行线,形成三个小三角形①、②、③,这三个小三角形面积分别为1、4、9,得到△GPF∽△PDE∽△HIP,△GPF∽△GDC,△GPF∽△AIF,△HIP∽△HBE,然后由相似三角形面积比等于相似比的平方,求得它们边长比为1:2:3,继而求得答案.
解:过△ABC内一点分别作三边的平行线,形成三个小三角形①、②、③,这三个小三角形面积分别为1、4、9,
∴△GPF∽△PDE∽△HIP,△GPF∽△GDC,△GPF∽△AIF,△HIP∽△HBE,
∴它们边长比为1:2:3,
∴S△GPF:S△GDC=1:9,S△GPF:S△AIF=1:16,S△HIP:S△HBE=9:25,
∴S四边形FPEC=9-1-4=4,S四边形AHPG=16-1-9=6,S△HBE=25,
∴S△ABC=S四边形FPEC+S四边形AHPG+S△HBE+S△GPF=4+6+25+1=36.
故答案为:36.

练习册系列答案
相关题目