Question

【题目】如图，矩形ABCD中，AB＝4，BC＝3，P在BA边上从B向A运动，过作PE⊥PC，交AD于点E．

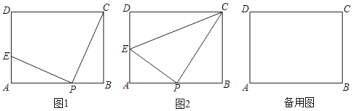
（1）如图1，当EP＝PC时，求线段AE的长度；

（2）如图2，当P为AB中点时，求证：CP平分∠ECB；

（3）若⊙O直径为CE，则在点P的运动过程中，是否存在⊙O与AB相切，若存在，求出⊙O的半径：若不存在，请说明理由．

Answer 1

【答案】（1）1；（2）见解析；（3）存在，⊙O的半径为 ．

【解析】

（1）如图1，先证明∠PEA=∠CPB，则根据“AAS”可判断△APE≌△BCP，从而得到AP=BC=3，AE=PB，然后计算出PB得到AE的长；
（2）如图2，先计算出PC=，再证明△APE∽△BCP，利用相似比计算出PE=，利用三角函数的定义得到tan∠ECP==tan∠BCP，从而可判断∠ECP=∠BCP；
（3）连接OP，如图3，根据切线的判定法，当OP⊥AB时，AB与⊙O相切，再证明AP=PB=2，则可利用由（2）的结论得到CP=，EP=，然后利用勾股定理计算出CE即可得到⊙O的半径．

（1）解：如图1，

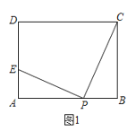
∵PE⊥PC，

∴∠EPC＝90°，

∴∠APE+∠CPB＝90°，

而∠APE+∠PEA＝90°，

∴∠PEA＝∠CPB，

在△APE和△BCP

，

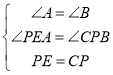∴△APE≌△BCP（AAS），

∴AP＝BC＝3，AE＝PB，

而PB＝AB﹣AP＝4﹣3＝1，

∴AE＝1；

（2）证明：如图2，

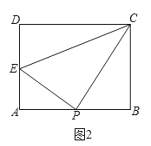
∵P为AB中点，

∴AP＝BP＝2，

∴PC＝，

∵∠PEA＝∠BPC，∠A＝∠B＝90°，

∴△APE∽△BCP，

∴，即，

解得：PE＝，

在Rt△PCE中，tan∠ECP＝，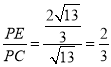

在Rt△PCB中，tan∠BCP＝，

∴∠ECP＝∠BCP，

∴CP平分∠ECB；

（3）解：存在．连接OP，如图3，

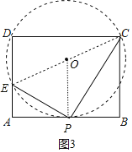
当OP⊥AB时，AB与⊙O相切，

∵OE＝OC，

∴AP＝PB＝2，

由（2）得CP＝，EP＝，

在Rt△PCE中，CE＝，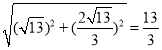

∴⊙O的半径为：.