题目内容
(本题满分12分)已知二次函数 的图象如图.
的图象如图.
(1)求它的对称轴与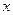 轴交点D的坐标;
轴交点D的坐标;
(2)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与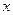 轴,
轴,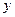 轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
轴的交点分别为A、B、C三点,若∠ACB=90°,求此时抛物线的解析式;
(3)设(2)中平移后的抛物线的顶点为M,以AB为直径,D为圆心作⊙D,试判断直线CM与⊙D的位置关系,并说明理由.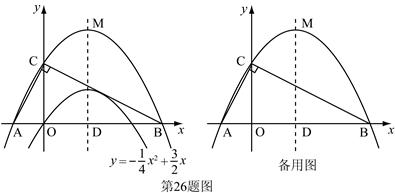
(本题满分12分)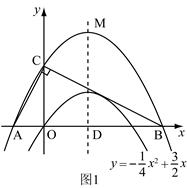 解: (1)由
解: (1)由 得
得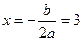
 …………1分
…………1分
∴D(3,0)…………2分
(2)方法一:
如图1, 设平移后的抛物线的解析式为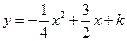 …………3分
…………3分
则C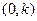 OC=
OC=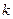
令 即
即 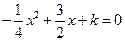
得 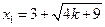
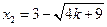 …………4分
…………4分
∴A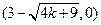 ,B
,B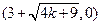
∴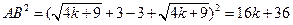 ………5分
………5分
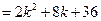 ……………………6分
……………………6分
∵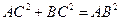
即: 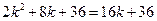
得 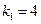
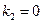 (舍去) ……………7分
(舍去) ……………7分
∴抛物线的解析式为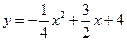 ……………8分
……………8分
方法二:
∵  ∴顶点坐标
∴顶点坐标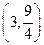
设抛物线向上平移h个单位,则得到 ,顶点坐标
,顶点坐标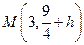 …………3分
…………3分
∴平移后的抛物线: 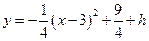 ……………………4分
……………………4分
当 时,
时,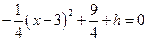 , 得
, 得 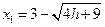
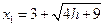
∴ A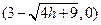 B
B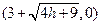 ……………………5分
……………………5分
∵∠ACB=90° ∴△AOC∽△COB
∴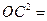 OA·OB……………………6分
OA·OB……………………6分 得
得 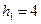 ,
,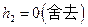 …………7分
…………7分
∴平移后的抛物线: 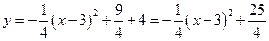 …………8分
…………8分
(3)方法一:
如图2,由抛物线的解析式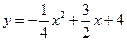 可得
可得
A(-2 ,0),B(8,0),C(4,0) ,M …………9分
…………9分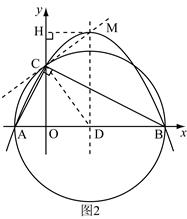 过C、M作直线,连结CD,过M作MH垂直y轴于H,
过C、M作直线,连结CD,过M作MH垂直y轴于H,
则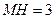
∴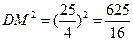
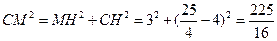
在Rt△COD中,CD=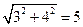 =AD
=AD
∴点C在⊙D上 ……… …………10分
…………10分
∵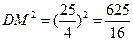
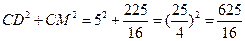 …
… …11分
…11分
∴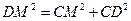
∴△CDM是直角三角形,∴CD⊥CM
∴直线CM与⊙D相切 …………12分
方法二:
如图3,由抛物线的解析式可得
A(-2 ,0),B(8,0),C(4,0) ,M …………9分
…………9分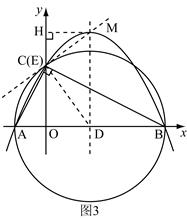 作直线CM,过D
作直线CM,过D 作DE⊥CM于E, 过M作MH垂直y轴于H,则
作DE⊥CM于E, 过M作MH垂直y轴于H,则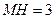 ,
, 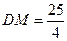 , 由勾股定理得
, 由勾股定理得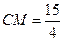
∵DM∥OC
∴∠MCH=∠EMD
∴Rt△CMH∽Rt△DME … ………10分
………10分
∴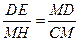 得
得 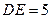 …………11分
…………11分
由(2)知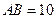 ∴⊙D的半径为5
∴⊙D的半径为5
∴直线CM与⊙D相切 …………12分
解析


 为平行四边形ABCD的对角线,
为平行四边形ABCD的对角线, 为
为 于点
于点 ,
, 分别交于点
分别交于点 .
.
 .
.

