Question

（本题满分12分）

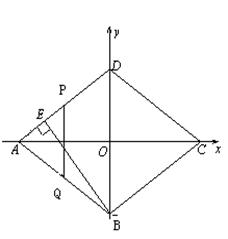
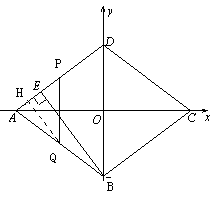
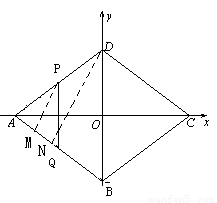
已知直角坐标系中菱形ABCD的位置如图，C，D两点的坐标分别为(4,0)，(0,3).现有两动点P,Q分别从A,C同时出发，点P沿线段AD向终点D运动，点Q沿折线CBA向终点A运动，设运动时间为t秒.

 

 

 

 

 

 

 

 

1.(1)填空：菱形ABCD的边长是   ▲   、面积是  ▲  、  高BE的长是  ▲   ；

2.(2)探究下列问题：

若点P的速度为每秒1个单位，点Q的速度为每秒2个单位.当点Q在线段BA上时

②  △APQ的面积S关于t的函数关系式，以及S的最大值；

3.（3）在运动过程中是否存在某一时刻使得△APQ为等腰三角形，若存在求出t的值；若不存在说明理由.

 

Answer 1

【答案】

 

1.(1)5 、 24 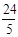 、………………………3分

2.(2) 过Q点作QH⊥AD于H

 证△AHQ∽AEB得HQ=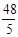-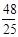t

      S=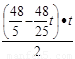

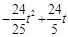      = …………………6分

     当t=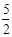时，S最大=6…………７分

 

 

3.(3)存在.………………８分

若AP=AQ

则t=10-2t

   t=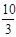

 

 

若PQ=AQ

过Q点作QH⊥AD于H

可证△AHQ∽AEB得AH=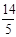-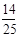t

AP=t

根据等腰三角形三线合一得AH=PH

∴AP=2AH

即

t=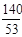

若AP=PQ

方法同PQ=AQ得t=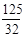………………11分

∵点Q在线段BA上,则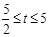

∴t= 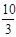、、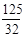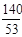都符合题意……………12分

 

 

 

 

【解析】略