Question

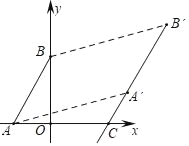
【题目】如图，已知A（﹣2，0），B（0，4），将线段AB平移到第一象限得线段A′B′，点A′的横坐标为5，若作直线A′B′交x轴于点C（4，0）．

（1）求线段AB所在直线的解析式；

（2）直线AB上一点P（m，n），求出m、n之间的数量关系；

（3）若点Q在y轴上，求QA′+QB′的取值范围．

Answer 1

【答案】（1）y＝2x+4；（2）n＝2m+4；（3）QA'+QB'≥4．

【解析】

（1）直接利用待定系数法即可得出结论；
（2）将点P的坐标代入直线AB的解析式中即可得出结论；
（3）先确定出直线A'B'的解析式，进而求出点A'，B'的坐标，再求出点A'关于y轴的对称点D的坐标，进而求出QA'+QB'的最小值，即可得出结论．

解：（1）设线段AB所在直线的解析式为y＝kx+b，

将A（﹣2，0），B（0，4）代入y＝kx+b中，，

∴，

∴线段AB所在直线的解析式为y＝2x+4；

（2）由（1）知，直线AB的解析式为y＝2x+4，

∵点P（m，n）在直线AB上，

∴n＝2m+4；

（3）如图，由（1）知，直线AB的解析式为y＝2x+4，

由平移，设直线A'B'的解析式为y＝2x+b'，

∵点C（4，0）在直线A'B'上，

∴2×4+b'＝0，

∴b'＝﹣8，

∴直线A'B'的解析式为y＝2x﹣8，

∵点A′的横坐标为5，

∴点A'（5，2），

∵A（﹣2，0），

∴点A'是点A向右移动5﹣（﹣2）＝7个单位，再向上平移2个单位所得，

∴点B'也是向右移动5﹣（﹣2）＝7个单位，再向上平移2个单位所得，

∵B（0，4），

∴B'（7，6），

作点A'关于y轴的对称点D（﹣5，2），

连接B'D，交y轴于Q，此时，QA'+QB'最小＝B'D＝

∴QA'+QB'≥4．