题目内容
【题目】已知抛物线C:y1=﹣x2+bx+4.
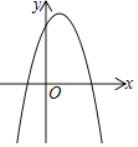
(1)如图,抛物线与x轴相交于两点(1﹣m,0)、(1+m,0).
①求b的值;
②当n≤x≤n+1时,二次函数有最大值为3,求n的值.
(2)已知直线l:y2=2x﹣b+9,当x≥0时,y1≤y2恒成立,求b的取值范围.
【答案】(1)b=2;(2)![]() 或
或![]() ;(3)b≤4.
;(3)b≤4.
【解析】
(1)由根与系数的关系得出x1+x2=-b,由抛物线与x轴的交点即为方程值为0的解,再将两个代入x1+x2=-b即可得到b的值.;
(2)需要分情况讨论,当n+1≤1,即n≤0;当n≤1≤n+1,即0≤n≤1;或n≥1三种情况,分别求解即可;
(3)将y1=﹣x2+bx+4,y2=2x﹣b+9代入y1≤y2整理得到x2+(2﹣b)x+5﹣b≥0,题意告知对于当x≥0时x2+(2﹣b)x+5﹣b≥0恒成立,故需分下面两种情况求解:①:△≤0,(2-b)2-4(5-b)≤0;②:△>0,则b>4或b<-4,即可求解.
解:(1)﹣x2+bx+4=0
![]() ,
,
b=2;
(2)抛物线开口向下,对称轴左侧y随x的增大而增大;对称轴右侧,y随x的增大而减小.
i:n+1≤1即n≤0,
当x=n+1时,y有最大值,
![]() ,
,
又∵n≤0,∴![]() ,
,
ii:n≤1≤n+1即0≤n≤1,
当x=1时y有最大值,
﹣12+2<1+4=3不成立,
iii:n≥1时,
当x=n时,y有最大值,
![]() ,
,
又∵n≥1,
∴![]() ,
,
综上所述:![]() 或
或![]() ;
;
(3)y1≤y2,
﹣x2+bx+4≤2x﹣b+9,
x2+(2﹣b)x+5﹣b≥0,
①:△≤0,
(2﹣b)2﹣4(5﹣b)≤0,
﹣4≤b≤4;
②:△>0则b>4或b<﹣4,
i:![]() ,不成立,
,不成立,
ii: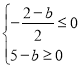 ,
,
b≤2,
又∵b>4或b<﹣4,
∴b<﹣4,
综上所述b≤4.

练习册系列答案
相关题目