题目内容
甲、乙两人同时登云雾山，甲、乙两人距地面的高度y（米）与登山时间x（分）之间的函数图象如图所示，若乙提速后乙的速度是甲的3倍，从甲、乙相距100米到乙追上甲时，甲、乙两人一共攀登了______米．
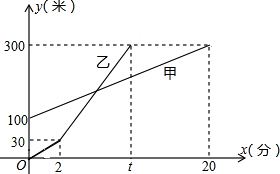
由图象得：
甲的速度为：（300-100）÷20=10米/分，
∴乙提速后乙的速度是30米/分
∴30（t-2）=300-30，
解得：t=11．
∴B（11，300）
设AB的解析式为y1=k1x+b2，CD的解析式为y2=k2x+b2，由题意，得
，
，
解得：
，
，
∴y1=30x-30，y2=10x+100，
当y1=y2时，
30x-30=10x+100，
解得：x=
，
y1=165，y2=165．
甲乙两人一共攀登的路程是：165+165-100=230米
故答案为：230
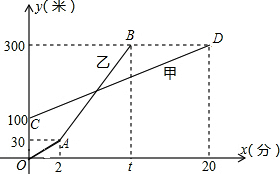
甲的速度为：（300-100）÷20=10米/分，
∴乙提速后乙的速度是30米/分
∴30（t-2）=300-30，
解得：t=11．
∴B（11，300）
设AB的解析式为y1=k1x+b2，CD的解析式为y2=k2x+b2，由题意，得
|
|
解得：
|
|
∴y1=30x-30，y2=10x+100，
当y1=y2时，
30x-30=10x+100，
解得：x=
| 13 |
| 2 |
y1=165，y2=165．
甲乙两人一共攀登的路程是：165+165-100=230米
故答案为：230
练习册系列答案
孟建平名校考卷系列答案
相关题目
交行李托运费．行李费托运费y（元）与行李重量x（千克）之间的函数关系如图所示．
x（时）的关系如图所示，根据图象回答：
