Question

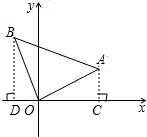
如图，Rt△ABC中，∠ABC=90°，OA=OB=1，与x轴的正方向夹角为30°．求直线AB的解析式．

Answer 1

作AC⊥x轴于C，BD⊥x轴D，
在Rt△AOC中，OC=1×cos30°=

3

2

，AC=

1

2

×1=

1

2

，
∴A点坐标为（

3

2

，

1

2

），
OD=1×cos60°=

1

2

，DB=1×sin60°=

3

2

，
∴B点坐标为（-

1

2

，

3

2

），
设解析式为y=kx+b，
把（

3

2

，

1

2

），（-

1

2

，

3

2

）分别代入解析式得：

3 2 k+b= 1 2 - 1 2 k+b= 3 2

，
解得k=-2+

3

，b=-1+

3

，
∴解析式为y=（-2+

3

）x+（-1+

3

）．