��Ŀ����
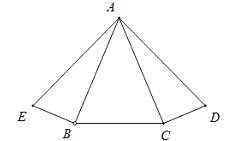
����Ŀ��ȡһ�������ε�ֽƬ�����۵�����������������£�
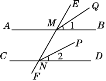
��һ������ͼ1���Ȱ�������ABCD���ۣ��ۺ�ΪMN��
�ڶ�������G���߶� MD�ϣ�����GCD��GC���ۣ���Dǡ������MN�ϣ���Ϊ��P������BP��
��1���жϡ�PBC����״����˵�����ɣ�
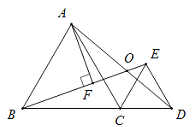
��2������C����ֱ��AP�ĶԳƵ�C�䣬����PC�䡢DC�䣮
����ͼ2�в�ȫͼ�Σ��������APC��Ķ�����
�ڲ����PC��D�Ķ�����������֤��������ܰ��ʾ��������������ʱ����������AC�䡢CC�䣬�о�ͼ��������������Σ�
���𰸡�
��1���⣺��PBC�ǵȱ������Σ��������£�
���ı���ABCD�������Σ�
��AB=BC=CD����ABC=90�㣬
���۵������ʵã�BN=NC= ![]() BC=
BC= ![]() PC��MN��BC��
PC��MN��BC��
��PB=PC����PNC=90�㣬
��Rt��PNC��sin��NPC= ![]() =
= ![]() ��
��
���NPC=30�㣬
���PCB=60�㣬
���PBC�ǵȱ�������
��2���⣺�ٲ�ȫͼ����ͼ2��ʾ��
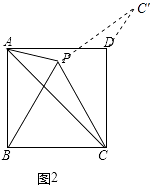
�ɢٵã���PCB=��PBC=��BPC=60�㣬PB=PC=BC��
�ߡ�ABC=90�㣬
���ABP=90�㩁60��=30�㣬
��AB=BC��
��AB=PB��
���BAP=��BPA= ![]() ��180�㩁30�㣩=75�㣬
��180�㩁30�㣩=75�㣬
���APC=��BPA+��BPC=75��+60��=135�㣬
��C����ֱ��AP�ĶԳƵ�ΪC�䣬
���APC'=��APC=135�㣻
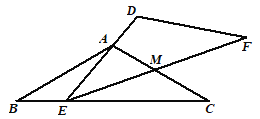
������AC'��CC'����ͼ3��ʾ��
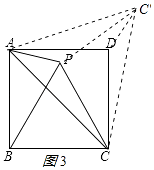
�ɶԳƵ����ʵã�AC=AC'����CAP=��C'AP=30�㣬
���CAC'=60�㣬
���CAC'�ǵȱ������Σ�
��AC'=CC'����AC'C=60�㣬
�ڡ�AC'D�͡�CC'D�У� 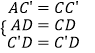 ��
��
���AC'D�ա�CC'D��SSS����
���AC'D=��CC'D= ![]() ��AC'C=30�㣬
��AC'C=30�㣬
�ߡ�AC'P=��ACP=15�㣬
���PC'D=15�㣮
����������1���������ε����ʵó�AB=BC=CD����ABC=90�㣬���۵������ʵã�BN=NC= ![]() BC=
BC= ![]() PC��MN��BC���ó�PB=PC����PNC=90�㣬��Rt��PNC�У������Ǻ����ó�sin��NPC=
PC��MN��BC���ó�PB=PC����PNC=90�㣬��Rt��PNC�У������Ǻ����ó�sin��NPC= ![]() =
= ![]() �������NPC=30�㣬�ó���PCB=60�㣬���ɵó����ۣ���2���ٸ������ⲹȫͼ�Σ��ɢٵã���PCB=��PBC=��BPC=60�㣬PB=PC=BC���ɵ��������ε����ʺ��������ڽǺͶ����ó���BAP=��BPA=75�㣬�����APC=��BPA+��BPC=135�㣬���ɵó������ʵó���APC'=��APC=135�㣻���ɶԳƵ����ʵã�AC=AC'����CAP=��C'AP=30�㣬֤����CAC'�ǵȱ������Σ��ó�AC'=CC'����AC'C=60�㣬��SSS֤����AC'D�ա�CC'D���ó���AC'D=��CC'D=
�������NPC=30�㣬�ó���PCB=60�㣬���ɵó����ۣ���2���ٸ������ⲹȫͼ�Σ��ɢٵã���PCB=��PBC=��BPC=60�㣬PB=PC=BC���ɵ��������ε����ʺ��������ڽǺͶ����ó���BAP=��BPA=75�㣬�����APC=��BPA+��BPC=135�㣬���ɵó������ʵó���APC'=��APC=135�㣻���ɶԳƵ����ʵã�AC=AC'����CAP=��C'AP=30�㣬֤����CAC'�ǵȱ������Σ��ó�AC'=CC'����AC'C=60�㣬��SSS֤����AC'D�ա�CC'D���ó���AC'D=��CC'D= ![]() ��AC'C=30�㣬�ɡ�AC'P=��ACP=15�㣬���ɵó���PC'D=15�㣮
��AC'C=30�㣬�ɡ�AC'P=��ACP=15�㣬���ɵó���PC'D=15�㣮
�����㾫����������Ҫ������ȫ�������ε����ʺ������ε����ʵ����֪ʶ�㣬��Ҫ����ȫ�������εĶ�Ӧ�����; ȫ�������εĶ�Ӧ����ȣ��������ĸ��Ƕ���ֱ�ǣ������߶���ȣ������ε������Խ�����ȣ����һ��ഹֱƽ�֣�ÿ���Խ���ƽ��һ��Խǣ������ε�һ���Խ��߰������ηֳ�����ȫ�ȵĵ���ֱ�������Σ������εĶԽ�����ߵļн���45o�������ε������Խ��߰���������ηֳ��ĸ�ȫ�ȵĵ���ֱ�������β�����ȷ�����⣮

 ��У���˿��ֿ���ϵ�д�
��У���˿��ֿ���ϵ�д�