题目内容
 (1998•大连)如图,在直角梯形ABCD中.AD∥BC,DC⊥BC,且BC=3AD.以梯形的高AE为直径的⊙O交AB于点F,交CD于点G、H.过点F引⊙O的切线交BC于点N.
(1998•大连)如图,在直角梯形ABCD中.AD∥BC,DC⊥BC,且BC=3AD.以梯形的高AE为直径的⊙O交AB于点F,交CD于点G、H.过点F引⊙O的切线交BC于点N.(1)求证:BN=EN;
(2)求证:4DH•HC=AB•BF;
(3)设∠GEC=α.若tan∠ABC=2,求作以tanα、cotα为根的一元二次方程.
分析:(1)首先连接OF,易证得△BFN是等腰三角形,且BN=FN,又由切线长定理,证得FN=EN,即可证得BN=EN;
(2)首先过点O作OK⊥GH于点K,由垂径定理可证得DG=HC,又由切割线定理,证得AD2=DH•DG,BE2=AB•BF,然后由BC=3AD,可得BE=2AD,继而证得4DH•HC=AB•BF;
(3)首先连接OG,由tan∠ABC=2,可设BE=2a,则AE=4a,继而求得EC与CG的长,根据正切函数与余切函数函数的定义,即可求得tanα、cotα的值,又由根与系数的关系,即可求得答案.
(2)首先过点O作OK⊥GH于点K,由垂径定理可证得DG=HC,又由切割线定理,证得AD2=DH•DG,BE2=AB•BF,然后由BC=3AD,可得BE=2AD,继而证得4DH•HC=AB•BF;
(3)首先连接OG,由tan∠ABC=2,可设BE=2a,则AE=4a,继而求得EC与CG的长,根据正切函数与余切函数函数的定义,即可求得tanα、cotα的值,又由根与系数的关系,即可求得答案.
解答: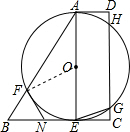 (1)证明:连接OF,
(1)证明:连接OF,
∵FN是⊙O的切线,
∴OF⊥FN,
即∠OFN=90°,
∴∠BFN+∠AFO=90°,
∵AE是梯形的高,
∴∠AEB=90°,
∴AE⊥BC,
∴∠BAE+∠B=90°,
∵OA=OF,
∴∠AFO=∠BAE,
∴∠B=∠BFN,
∴BN=FN,
∵AE为⊙O的直径,
∴BC是⊙O的切线,
∴FN=EN,
BN=EN;
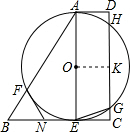 (2)过点O作OK⊥GH于点K,
(2)过点O作OK⊥GH于点K,
∴KH=KG,
∵AE为⊙O的直径,且AE是梯形的高,
∴AD是⊙O得切线,且AD∥OK∥EC,
∴AD2=DH•DG,DK=CK,
∴DG=HC,
∴AD2=DH•HC;
∵BC是⊙O的切线,
∴BE2=AB•BF,
∵在直角梯形ABCD中.AD∥BC,DC⊥BC,
∴四边形ADCE是矩形,
∴EC=AD,
∵BC=3AD,
∴BE=2AD,
∴4AD2=AB•BF,
∴4DH•HC=AB•BF;
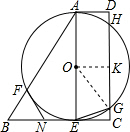 (3)连接OG,
(3)连接OG,
∵在Rt△ABE中,tan∠ABC=
=2,
∴设BE=2a,则AE=4a,
∴CK=OG=
AE=2a,OK=EC=
BE=a,
在Rt△OKG中,KG=
=
a,
∴CG=CK-KG=(2-
)a,
在Rt△ECG中,tanα=
=2-
,cotα=
=2+
,
∴tanα+cotα=4,tanα•cotα=1,
∴以tanα、cotα为根的一元二次方程为:x2-4x+1=0.
 (1)证明:连接OF,
(1)证明:连接OF,∵FN是⊙O的切线,
∴OF⊥FN,
即∠OFN=90°,
∴∠BFN+∠AFO=90°,
∵AE是梯形的高,
∴∠AEB=90°,
∴AE⊥BC,
∴∠BAE+∠B=90°,
∵OA=OF,
∴∠AFO=∠BAE,
∴∠B=∠BFN,
∴BN=FN,
∵AE为⊙O的直径,
∴BC是⊙O的切线,
∴FN=EN,
BN=EN;
 (2)过点O作OK⊥GH于点K,
(2)过点O作OK⊥GH于点K,∴KH=KG,
∵AE为⊙O的直径,且AE是梯形的高,
∴AD是⊙O得切线,且AD∥OK∥EC,
∴AD2=DH•DG,DK=CK,
∴DG=HC,
∴AD2=DH•HC;
∵BC是⊙O的切线,
∴BE2=AB•BF,
∵在直角梯形ABCD中.AD∥BC,DC⊥BC,
∴四边形ADCE是矩形,
∴EC=AD,
∵BC=3AD,
∴BE=2AD,
∴4AD2=AB•BF,
∴4DH•HC=AB•BF;
 (3)连接OG,
(3)连接OG,∵在Rt△ABE中,tan∠ABC=
| AE |
| BE |
∴设BE=2a,则AE=4a,
∴CK=OG=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△OKG中,KG=
| OG2-OK2 |
| 3 |
∴CG=CK-KG=(2-
| 3 |
在Rt△ECG中,tanα=
| CG |
| EC |
| 3 |
| EC |
| CG |
| 3 |
∴tanα+cotα=4,tanα•cotα=1,
∴以tanα、cotα为根的一元二次方程为:x2-4x+1=0.
点评:此题考查了切线的判定与性质、切割线定理、切线长定理、垂径定理、直角梯形的性质、勾股定理、根与系数的关系以及三角函数等知识.此题综合性很强,难度较大,注意掌握辅助线的作法,注意数形结合思想与方程思想的应用.

练习册系列答案
相关题目
 (1998•大连)如图,PC切⊙O于点C,割线PAB交⊙O于点A、B,若PA=2,AB=4,则BC2:AC2的值为( )
(1998•大连)如图,PC切⊙O于点C,割线PAB交⊙O于点A、B,若PA=2,AB=4,则BC2:AC2的值为( ) (1998•大连)如图,AB是半圆O的直径,AC是弦,D是弧AC的中点,若∠BAC=26°,则∠DCA的度数是( )
(1998•大连)如图,AB是半圆O的直径,AC是弦,D是弧AC的中点,若∠BAC=26°,则∠DCA的度数是( ) (1998•大连)如图,AB是半圆O的直径,点C、D是半圆O的三等分点,如果BC=3,那么图中阴影部分的面积为
(1998•大连)如图,AB是半圆O的直径,点C、D是半圆O的三等分点,如果BC=3,那么图中阴影部分的面积为 (1998•大连)如图,∠AOC=60°,点B在OA上且OB=2
(1998•大连)如图,∠AOC=60°,点B在OA上且OB=2