题目内容
已知:在如图1所示的锐角三角形ABC中,CH⊥AB于点H,点B关于直线CH的对称点为D,AC边上一点E满足∠EDA=∠A,直线DE交直线CH于点F.
(1)求证:BF∥AC;
(2)若AC边的中点为M,求证:DF=2EM;
(3)当AB=BC时(如图2),在未添加辅助线和其它字母的条件下,找出图2中所有与BE相等的线段,并证明你的结论.

(1)求证:BF∥AC;
(2)若AC边的中点为M,求证:DF=2EM;
(3)当AB=BC时(如图2),在未添加辅助线和其它字母的条件下,找出图2中所有与BE相等的线段,并证明你的结论.

分析:(1)根据点B与点D关于关于直线CH的对称,可得BF=DF,根据等边对等角可得∠1=∠2,再证明∠A=∠2,再根据内错角相等,两直线平行可证出AC∥FB;
(2)首先取FD的中点N,连接HM、HN,再证明四边形ENHM是平行四边形,由平行四边形的性质可得HN=EM,在Rt△DFH中,∠DHF=90°,DF的中点为N,根据直角三角形中斜边上的中线等于斜边的一半可得NH=
DF,再利用等量代换可得DF=2EM;
(3)当AB=BC时,在未添加辅助线和其它字母的条件下,原题图2中所有与BE相等的线段是EF和CE.连接CD,证明△ABE≌△DCE可得BE=CE;由BF=DF得∠CFE=∠BFC.由所得BF∥AC 可得∠BFC=∠ECF,进而得到∠CFE=∠ECF,可得EF=CE,即可得到BE=EF=CE.
(2)首先取FD的中点N,连接HM、HN,再证明四边形ENHM是平行四边形,由平行四边形的性质可得HN=EM,在Rt△DFH中,∠DHF=90°,DF的中点为N,根据直角三角形中斜边上的中线等于斜边的一半可得NH=
| 1 |
| 2 |
(3)当AB=BC时,在未添加辅助线和其它字母的条件下,原题图2中所有与BE相等的线段是EF和CE.连接CD,证明△ABE≌△DCE可得BE=CE;由BF=DF得∠CFE=∠BFC.由所得BF∥AC 可得∠BFC=∠ECF,进而得到∠CFE=∠ECF,可得EF=CE,即可得到BE=EF=CE.
解答: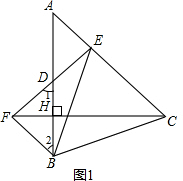 证明:(1)如图1.
证明:(1)如图1.
∵点B关于直线CH的对称点为D,CH⊥AB于点H,直线DE交直线CH于点F,
∴BF=DF,DH=BH.
∴∠1=∠2.
又∵∠EDA=∠A,∠EDA=∠1,
∴∠A=∠2.
∴BF∥AC;
(2)如图2,取FD的中点N,连接HM、HN.
∵H是BD的中点,N是FD的中点,
∴HN∥BF.
由(1)得BF∥AC,
∴HN∥AC,即HN∥EM.
∵在Rt△ACH中,∠AHC=90°,AC边的中点为M,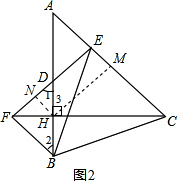
∴HM=
AC=AM,
∴∠A=∠3,
∴∠EDA=∠3,
∴NE∥HM,
∴四边形ENHM是平行四边形,
∴HN=EM,
∵在Rt△DFH中,∠DHF=90°,DF的中点为N,
∴HN=
DF,即DF=2HN,
∴DF=2EM;
(3)当AB=BC时,在未添加辅助线和其它字母的条件下,原题图2中所有与BE相等的线段是EF和CE.
证明:连接CD.(如图3)
∵点B关于直线CH的对称点为D,CH⊥AB于点H,
∴BC=CD,∠ABC=∠5.
∵AB=BC,
∴∠ABC=180°-2∠A,
AB=CD.①
∵∠EDA=∠A,
∴∠6=180°-2∠A,AE=DE.②
∴∠ABC=∠6=∠5.
∵∠BDE是△ADE的外角,
∴∠BDE=∠A+∠6.
∵∠BDE=∠4+∠5,
∴∠A=∠4.③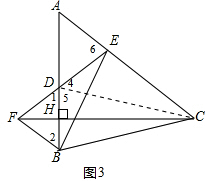
由①,②,③得△ABE≌△DCE.
∴BE=CE.
由(1)中BF=DF得∠CFE=∠BFC.
由(1)中所得BF∥AC 可得∠BFC=∠ECF.
∴∠CFE=∠ECF.
∴EF=CE.
∴BE=EF.
∴BE=EF=CE.
 证明:(1)如图1.
证明:(1)如图1.∵点B关于直线CH的对称点为D,CH⊥AB于点H,直线DE交直线CH于点F,
∴BF=DF,DH=BH.
∴∠1=∠2.
又∵∠EDA=∠A,∠EDA=∠1,
∴∠A=∠2.
∴BF∥AC;
(2)如图2,取FD的中点N,连接HM、HN.
∵H是BD的中点,N是FD的中点,
∴HN∥BF.
由(1)得BF∥AC,
∴HN∥AC,即HN∥EM.
∵在Rt△ACH中,∠AHC=90°,AC边的中点为M,

∴HM=
| 1 |
| 2 |
∴∠A=∠3,
∴∠EDA=∠3,
∴NE∥HM,
∴四边形ENHM是平行四边形,
∴HN=EM,
∵在Rt△DFH中,∠DHF=90°,DF的中点为N,
∴HN=
| 1 |
| 2 |
∴DF=2EM;
(3)当AB=BC时,在未添加辅助线和其它字母的条件下,原题图2中所有与BE相等的线段是EF和CE.
证明:连接CD.(如图3)
∵点B关于直线CH的对称点为D,CH⊥AB于点H,
∴BC=CD,∠ABC=∠5.
∵AB=BC,
∴∠ABC=180°-2∠A,
AB=CD.①
∵∠EDA=∠A,
∴∠6=180°-2∠A,AE=DE.②
∴∠ABC=∠6=∠5.
∵∠BDE是△ADE的外角,
∴∠BDE=∠A+∠6.
∵∠BDE=∠4+∠5,
∴∠A=∠4.③

由①,②,③得△ABE≌△DCE.
∴BE=CE.
由(1)中BF=DF得∠CFE=∠BFC.
由(1)中所得BF∥AC 可得∠BFC=∠ECF.
∴∠CFE=∠ECF.
∴EF=CE.
∴BE=EF.
∴BE=EF=CE.
点评:此题主要考查了平行四边形的判定与性质,关键是熟练掌握平行四边形的判定方法以及平行四边形的性质定理.

练习册系列答案
相关题目