题目内容
(2013•徐州模拟)已知:在如图1所示的平面直角坐标系xOy中,A、C两点的坐标分别为A(4,2),C(n,-2)(其中n>0),点B在x轴的正半轴上.动点P从点O出发,在四边形OABC的边上依次沿O-A-B-C的顺序向点C移动,当点P与点C重合时停止运动.设点P移动的路径的长为l,△POC的面积为S,S与l的函数关系的图象如图2所示,其中四边形ODEF是等腰梯形.
(1)结合以上信息及图2填空:图2中的m=
(2)求B、C两点的坐标及图2中OF的长;
(3)若OM是∠AOB的角平分线,且点G与点H分别是线段AO与射线OM上的两个动点,直接写出HG+AH的最小值,请在图3中画出示意图并简述理由.

(1)结合以上信息及图2填空:图2中的m=
2
| 5 |
2
;| 5 |
(2)求B、C两点的坐标及图2中OF的长;
(3)若OM是∠AOB的角平分线,且点G与点H分别是线段AO与射线OM上的两个动点,直接写出HG+AH的最小值,请在图3中画出示意图并简述理由.

分析:(1)由四边形ODEF是等腰梯形,易得四边形OABC是平行四边形,由图2可得S△AOC=8,连接AC交x轴于R点,易得OR=4,由勾股定理可求得OA的值,即m的值;
(2)由OB=2RO=8,AR⊥OB,即可求得B、C两点的坐标,易证得平行四边形OABC是菱形,则可得OF=3OA;
(3)在OB上找一点N使ON=OG,连接NH,易证得△GOH≌△NOH,则可得GH+AH=AH+HN,根据垂线段最短可知:当AN是点A到OB的垂线段时,且H点是AN与OM的交点,继而求得答案.
(2)由OB=2RO=8,AR⊥OB,即可求得B、C两点的坐标,易证得平行四边形OABC是菱形,则可得OF=3OA;
(3)在OB上找一点N使ON=OG,连接NH,易证得△GOH≌△NOH,则可得GH+AH=AH+HN,根据垂线段最短可知:当AN是点A到OB的垂线段时,且H点是AN与OM的交点,继而求得答案.
解答: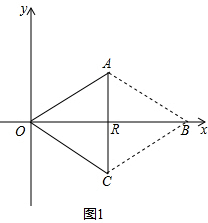 解:(1)如图1,∵四边形ODEF是等腰梯形,
解:(1)如图1,∵四边形ODEF是等腰梯形,
∴OA=BC且OA∥BC,
∴四边形OABC是平行四边形,
由已知可得:S△AOC=8,连接AC交x轴于R点,
又∵A(4,2),C(n,-2),
∴S△AOC=S△AOR+S△ROC=0.5×RO×2+0.5×RO×2=2RO=8,
∴OR=4,
∴m=OA=
=
=2
;
故答案为:2
;
(2)∵OB=2RO=8,CR=AR=2,AR⊥OB,
∴B(8,0),C(4,-2)且平行四边形OABC是菱形,
∴OF=3AO=3×2
=6
;
(3)如图3,在OB上找一点N使ON=OG,连接NH,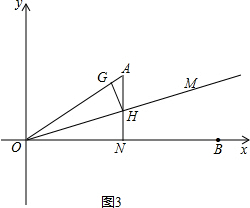
∵OM平分∠AOB,
∴∠AOM=∠BOM,
在△GOH和△NOH中,
,
∴△GOH≌△NOH(SAS),
∴GH=NH,
∴GH+AH=AH+HN=AN,
根据垂线段最短可知:当AN是点A到OB的垂线段时,且H点是AN与OM的交点,
∴GH+AH的最小值为2.
 解:(1)如图1,∵四边形ODEF是等腰梯形,
解:(1)如图1,∵四边形ODEF是等腰梯形,∴OA=BC且OA∥BC,
∴四边形OABC是平行四边形,
由已知可得:S△AOC=8,连接AC交x轴于R点,
又∵A(4,2),C(n,-2),
∴S△AOC=S△AOR+S△ROC=0.5×RO×2+0.5×RO×2=2RO=8,
∴OR=4,
∴m=OA=
| OR2+AR2 |
| 42+22 |
| 5 |
故答案为:2
| 5 |
(2)∵OB=2RO=8,CR=AR=2,AR⊥OB,
∴B(8,0),C(4,-2)且平行四边形OABC是菱形,
∴OF=3AO=3×2
| 5 |
| 5 |
(3)如图3,在OB上找一点N使ON=OG,连接NH,

∵OM平分∠AOB,
∴∠AOM=∠BOM,
在△GOH和△NOH中,
|
∴△GOH≌△NOH(SAS),
∴GH=NH,
∴GH+AH=AH+HN=AN,
根据垂线段最短可知:当AN是点A到OB的垂线段时,且H点是AN与OM的交点,
∴GH+AH的最小值为2.
点评:此题等腰梯形的性质、平行四边形的性质、菱形的判定与性质、勾股定理、全等三角形的判定与性质以及最短路径问题.此题难度较大,注意掌握数形结合思想的应用是解此题的关键.

练习册系列答案
相关题目
 (2013•徐州模拟)如图所示,甲、乙两船同时由港口A出发开往海岛B,甲船沿东北方向向海岛B航行,其速度为15海里/小时;乙船速度为20海里/小时,先沿正东方向航行1小时后,到达C港口接旅客,停留半小时后再转向北偏东30°方向开往B岛,其速度仍为20海里/小时.
(2013•徐州模拟)如图所示,甲、乙两船同时由港口A出发开往海岛B,甲船沿东北方向向海岛B航行,其速度为15海里/小时;乙船速度为20海里/小时,先沿正东方向航行1小时后,到达C港口接旅客,停留半小时后再转向北偏东30°方向开往B岛,其速度仍为20海里/小时.