题目内容
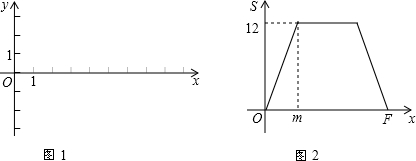
已知:在如图1所示的平面直角坐标系xOy中,A、C两点的坐标分别为A(4,2),C(n,-2)(其中n>0),点B在x轴的正半轴上.动点P从点O出发,在四边形OABC的边上依次沿O-A-B-C的顺序向点C移动,当点P与点C重合时停止运动.设点P移动的路径的长为l,△POC的面积为S,S与l的函数关系的图象如图2所示,其中四边形ODEF是等腰梯形.

(1)结合以上信息及图2填空:图2中的m=
(2)求B、C两点的坐标及图2中OF的长.

(1)结合以上信息及图2填空:图2中的m=
2
| 5 |
2
;| 5 |
(2)求B、C两点的坐标及图2中OF的长.
分析:(1)利用当P点运动到A点时,△POC的面积为12,求出斜边AO即可;
(2)图1中四边形ODEF是等腰梯形,点D的坐标为D(m,8),得出yE=yD=8,此时图2中点P运动到与点B重合,根据点P在AB上运动时△POC的面积不变,可得AB与OC平行,求出直线AB的解析式,可得出直线OC的解析式,再由点C纵坐标为-2,可确定点C的坐标,继而求出OF的长度.
(2)图1中四边形ODEF是等腰梯形,点D的坐标为D(m,8),得出yE=yD=8,此时图2中点P运动到与点B重合,根据点P在AB上运动时△POC的面积不变,可得AB与OC平行,求出直线AB的解析式,可得出直线OC的解析式,再由点C纵坐标为-2,可确定点C的坐标,继而求出OF的长度.
解答:解:(1)根据图形可得:当点P运动到点A时,△POC的面积为8,
∵OA=
=2
,
∴P移动的路径的长l=2
,
∴m的值为2
.
(2)∵图1中四边形ODEF是等腰梯形,点D的坐标为D(m,8),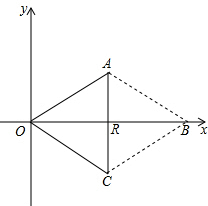
∴yE=yD=8,此时图2中点O运动到与点B重合,
∵点B在x轴上,
∴S△POC=
OB×2=8,
解得:OB=8,
即点B的坐标为(8,0),
∵点P在AB上运动时,△POC的面积不变,
∴可得OC∥AB,
设直线AB的解析式为y=kx+b,
将A、B的坐标代入可得:
,
解得:
,
∴直线AB的解析式为y=-
x+4,
∴直线OC的解析式为y=-
x,
∵点C的纵坐标为-2,
∴点C的横坐标为4,
∴点C的坐标为(4,-2),
∴OF=l=OA+AB+BC=2
+2
+2
=6
.
∵OA=
| 42+22 |
| 5 |
∴P移动的路径的长l=2
| 5 |
∴m的值为2
| 5 |
(2)∵图1中四边形ODEF是等腰梯形,点D的坐标为D(m,8),

∴yE=yD=8,此时图2中点O运动到与点B重合,
∵点B在x轴上,
∴S△POC=
| 1 |
| 2 |
解得:OB=8,
即点B的坐标为(8,0),
∵点P在AB上运动时,△POC的面积不变,
∴可得OC∥AB,
设直线AB的解析式为y=kx+b,
将A、B的坐标代入可得:
|
解得:
|
∴直线AB的解析式为y=-
| 1 |
| 2 |
∴直线OC的解析式为y=-
| 1 |
| 2 |
∵点C的纵坐标为-2,
∴点C的横坐标为4,
∴点C的坐标为(4,-2),
∴OF=l=OA+AB+BC=2
| 5 |
| 5 |
| 5 |
| 5 |
点评:本题考查了动点问题的函数图象,涉及了等腰梯形的性质、平行线的性质及一次函数的知识,综合性较强,解答本题关键是将两图中的点对应起来,此题难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目