题目内容
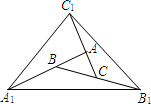如图，已知△ABC的面积为5，对△ABC进行以下操作：延长AB至点A1，使BA1=2AB；延长BC至点B1，使CB1=2BC；延长CA至点C1，使AC1=2CA；再顺次连接点A1、B1、C1得到△A1B1C1，若△A1B1C1 的面积为S，则S=95
95
．分析：连接A1C，根据图示可知△AA1C与△ABC是同高的两个三角形，由题意可以求得S△AA1C=3S△ABC=15，则S△AA1C1=2S△AA1C=30．S△A1B1C1=3S△AA1C1+S△ABC=19S△ABC．
解答：
解：如图，连接A1C．
∵BA1=2AB，
∴AA1=3AB，
S△AA1C=3S△ABC，
S△AA1C1=2S△AA1C=6S△ABC，
所以S△A1B1C1=3S△AA1C1+S△ABC=19S△ABC=19×5=95，即S=95．
故答案是：95．
解：如图，连接A1C．∵BA1=2AB，
∴AA1=3AB，
S△AA1C=3S△ABC，
S△AA1C1=2S△AA1C=6S△ABC，
所以S△A1B1C1=3S△AA1C1+S△ABC=19S△ABC=19×5=95，即S=95．
故答案是：95．
点评：本题考查了三角形的面积．解答此题的难点是将所求三角形的面积与已知三角形的面积的数量关系找出来．
练习册系列答案
相关题目
如图，已知△ABC的面积为4，且AB=AC，现将△ABC沿CA方向平移CA的长度，得到△EFA．
（2010•孝感模拟）如图，已知△ABC的三个顶点的坐标分别为A（-2，2）、B（-5，0）、C（-1，0）．
如图，已知△ABC的三个顶点的坐标分别是A（-7，1），B（-3，3），C（-2，6）．