题目内容
如图，已知△ABC的面积S△ABC=1．在图1中，若
| AA1 |
| AB |
| BB1 |
| BC |
| CC1 |
| CA |
| 1 |
| 2 |
| 1 |
| 4 |
在图2中，若
| AA2 |
| AB |
| BB2 |
| BC |
| CC2 |
| CA |
| 1 |
| 3 |
| 1 |
| 3 |
在图3中，若
| AA3 |
| AB |
| BB3 |
| BC |
| CC3 |
| CA |
| 1 |
| 4 |
| 7 |
| 16 |
按此规律，若
| AA8 |
| AB |
| BB8 |
| BC |
| CC8 |
| CA |
| 1 |
| 9 |
分析：根据图的特点，找出图中的相似三角形，求出其相似比，根据面积比等于相似比的平方找出规律解答．
解答：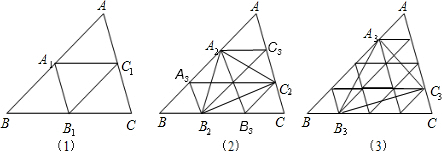
解：对图（2）进行分析：可以标出每条边的所有分点的字母，从A2开始，逆时针为A3、B3、C3，
可以得到△A3BB2∽△ABC，
且面积比为(
)2=
，也就可以得到S△A3BB2=
S△ABC，而△A2A3B2和△A3BB2同底等高，面积相等，
所以，S△A2BB2=
S△ABC，同样道理，可得到，S△B2C2C=
S△ABC，S△AA2C2=
S△ABC，
那么S△A2B2C3=（1-
）S△ABC=
S△ABC．
根据上述分析可以得到，如果An-1是AB的n等分点，Bn-1是BC的n等分点，Cn-1是AC的n等分点，
那么S△An-1Bn-1Cn-1=1-(
)2×3×(n-1)=1-
，当n=9时，则S△A8B8C8=1-
=
．
解：对图（2）进行分析：可以标出每条边的所有分点的字母，从A2开始，逆时针为A3、B3、C3，
可以得到△A3BB2∽△ABC，
且面积比为(
| 1 |
| 3 |
| 1 |
| 9 |
| 1 |
| 9 |
所以，S△A2BB2=
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
| 9 |
那么S△A2B2C3=（1-
| 6 |
| 9 |
| 1 |
| 3 |
根据上述分析可以得到，如果An-1是AB的n等分点，Bn-1是BC的n等分点，Cn-1是AC的n等分点，
那么S△An-1Bn-1Cn-1=1-(
| 1 |
| n |
| 3(n-1) |
| n2 |
| 3(9-1) |
| 81 |
| 19 |
| 27 |
点评：此题运用了相似三角形的判定和性质，以及相似三角形的面积比等于相似比的平方，还用到了等底等高的三角形面积相等的知识．
练习册系列答案
相关题目
如图，已知△ABC的面积为4，且AB=AC，现将△ABC沿CA方向平移CA的长度，得到△EFA．
（2010•孝感模拟）如图，已知△ABC的三个顶点的坐标分别为A（-2，2）、B（-5，0）、C（-1，0）．
如图，已知△ABC的三个顶点的坐标分别是A（-7，1），B（-3，3），C（-2，6）．