题目内容
(2012•温州二模)如图,已知△ABC的面积是2平方厘米,△BCD的面积是3平方厘米,△CDE的面积是3平方厘米,△DEF的面积是4平方厘米,△EFG的面积是3平方厘米,△FGH的面积是5平方厘米,那么,△EFH的面积是

4
4
平方厘米.
分析:先过点E作EM⊥AH,GN⊥AH,垂足分别为M,N,得出S△AEF和S△AGF的面积,从而得出
的值,再根据S△AEF=
AF•EM,S△AGF=
AF•NG,得出
=
,最后根据S△GFH=
FH•NG,S△EFH=
FH•EM,得出
的值,即可得出S△EFH的面积.
| S△AEF |
| S△AGF |
| 1 |
| 2 |
| 1 |
| 2 |
| EM |
| NG |
| 4 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| S△EFH |
| S△GFH |
解答: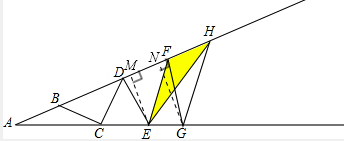 解:过点E作EM⊥AH,GN⊥AH,垂足分别为M,N,
解:过点E作EM⊥AH,GN⊥AH,垂足分别为M,N,
∵S△AEF=S△ABC+S△BCD+S△CDE+S△DEF=2+3+3+4=12(平方厘米),
S△AGF=S△ABC+S△BCD+S△CDE+S△DEF+S△EFG=2+3+3+4+3=15(平方厘米),
∴
=
=
,
∵S△AEF=
AF•EM,S△AGF=
AF•NG,
∴
=
,
∴
=
,
∵S△GFH=
FH•NG,S△EFH=
FH•EM,
∴
=
=
,
∴S△EFH=
×S△GFH=
×5=4(平方厘米);
故答案为:4.
 解:过点E作EM⊥AH,GN⊥AH,垂足分别为M,N,
解:过点E作EM⊥AH,GN⊥AH,垂足分别为M,N,∵S△AEF=S△ABC+S△BCD+S△CDE+S△DEF=2+3+3+4=12(平方厘米),
S△AGF=S△ABC+S△BCD+S△CDE+S△DEF+S△EFG=2+3+3+4+3=15(平方厘米),
∴
| S△AEF |
| S△AGF |
| 12 |
| 15 |
| 4 |
| 5 |
∵S△AEF=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| ||
|
| 4 |
| 5 |
∴
| EM |
| NG |
| 4 |
| 5 |
∵S△GFH=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| S△EFH |
| S△GFH |
| EM |
| NG |
| 4 |
| 5 |
∴S△EFH=
| 4 |
| 5 |
| 4 |
| 5 |
故答案为:4.
点评:此题考查了三角形的面积,解题的关键是求出△EFH和△GFH的高之比,解决此类问题时,要抓住问题开始逆向分析,找出与要求的三角形面积有关的已知条件.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 (2012•温州二模)如图,点D在以AC为直径的⊙O上,若∠BDC=35°,那么∠ACB=
(2012•温州二模)如图,点D在以AC为直径的⊙O上,若∠BDC=35°,那么∠ACB=