题目内容
 如图,已知△ABC的面积为4,且AB=AC,现将△ABC沿CA方向平移CA的长度,得到△EFA.
如图,已知△ABC的面积为4,且AB=AC,现将△ABC沿CA方向平移CA的长度,得到△EFA.(1)判断AF与BE的位置关系,并说明理由;
(2)若∠BEC=15°,求AC的长.
分析:(1)首先连接BF,由△AEF是由△ABC沿CA的方向平移CA长度得到,即可得BF=AC,AB=EF,CA=AE,又由AB=AC,证得AB=BF=EF=AE,根据由四条边都相等的四边形是菱形,即可证得四边形ABFE是菱形,则可得AF⊥BE;
(2)首先作BM⊥AC于点M,由AB=AC=AE,∠BEC=15°,求得∠BAC=30°,BM=
AB=
AC,然后利用△ABC的面积求解方法,即可求得AC的长.
(2)首先作BM⊥AC于点M,由AB=AC=AE,∠BEC=15°,求得∠BAC=30°,BM=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解: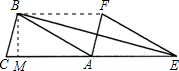 (1)AF⊥BE.
(1)AF⊥BE.
理由如下:连接BF,
∵△AEF是由△ABC沿CA的方向平移CA长度得到,
∴BF=AC,AB=EF,CA=AE.
∵AB=AC,
∴AB=BF=EF=AE.
∴四边形ABFE是菱形.
∴AF⊥BE.
(2)作BM⊥AC于点M.
∵AB=AC=AE,∠BEC=15°,
∴∠BAC=30°.
∴BM=
AB=
AC.
∵S△ABC=4,
∴
•AC•
AC=4,
∴AC=4.
 (1)AF⊥BE.
(1)AF⊥BE.理由如下:连接BF,
∵△AEF是由△ABC沿CA的方向平移CA长度得到,
∴BF=AC,AB=EF,CA=AE.
∵AB=AC,
∴AB=BF=EF=AE.
∴四边形ABFE是菱形.
∴AF⊥BE.
(2)作BM⊥AC于点M.
∵AB=AC=AE,∠BEC=15°,
∴∠BAC=30°.
∴BM=
| 1 |
| 2 |
| 1 |
| 2 |
∵S△ABC=4,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴AC=4.
点评:此题考查了菱形的判定与性质,三角形面积的求解方法等知识.此题难度不大,注意辅助线的作法与数形结合思想的应用.

练习册系列答案
相关题目


 (2010•孝感模拟)如图,已知△ABC的三个顶点的坐标分别为A(-2,2)、B(-5,0)、C(-1,0).
(2010•孝感模拟)如图,已知△ABC的三个顶点的坐标分别为A(-2,2)、B(-5,0)、C(-1,0). 如图,已知△ABC的三个顶点的坐标分别是A(-7,1),B(-3,3),C(-2,6).
如图,已知△ABC的三个顶点的坐标分别是A(-7,1),B(-3,3),C(-2,6).