��Ŀ����
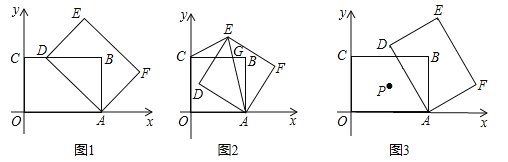
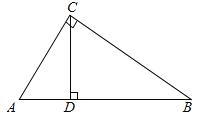
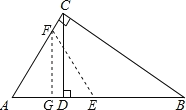
����Ŀ���ڡ�ABC�У���C��90����AC��3��BC��4��CD��б��AB�ϵĸߣ���E��б��AB�ϣ�����E��ֱ�����ABC��ֱ�DZ��ཻ�ڵ�F����AE��x����AEF�����Ϊy��
��1��CD= ��AD= ��
��2����EF��AB������E���߶�AB���ƶ�ʱ��
����y��x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
�ڵ�xȡ��ֵʱ��y�����ֵ�����������ֵ
��3����F��ֱ�DZ�AC�ϣ���F��A��C��������غϣ�����E��б��AB���ƶ������ʣ��Ƿ����ֱ��EF����ABC���ܳ������ͬʱƽ�֣�������ֱ��EF�����x��ֵ����������ֱ��EF����˵�����ɣ�
���𰸡���1��![]() ��
��![]() ����2����
����2����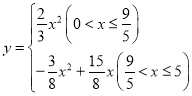 ���ڵ�x��
���ڵ�x��![]() ��5ʱ��
��5ʱ��![]() �����
�����![]() ����3�����ڣ�
����3�����ڣ�![]()
��������
��1���ȸ��ݹ��ɶ������AB�ij����ٸ���Rt��ADC��Rt��ACB�����������Ʊȼ������AD�ij���
��2�����ֱ����x��ȡֵ��Χ�������ε������ʽ����ɵ�x��y�ĺ�����ϵʽ��
��������������ĺ�����ϵʽ�������ֵ���ɣ�
��3������á�ABC�������![]() �������õ���AEF�õ�����ĺ�����ϵʽ����������3����ʽ������⣮
�������õ���AEF�õ�����ĺ�����ϵʽ����������3����ʽ������⣮
�⣺��1���ߡ�ABC�У���C��90�㣬AC��3��BC��4��
��AB��![]() ��5��
��5��
��CD��AB��
���CDA����ACB��90�㣬
�֡�CAD����CAD��
��Rt��ADC��Rt��ACB��
��![]() ����
����![]() ��
��
��CD��![]() ��AD��
��AD��![]() ��
��
��2��������E��λ�ò���ȷ������Ӧ������������ۣ�
��ͼA����0��x��AD����0��x��![]() ʱ��
ʱ��
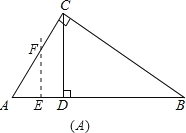
��EF��AB��
��Rt��AEF��Rt��ACB����![]() ��
��
��AC��3��BC��4��AE��x��
��![]() ��EF��
��EF��![]() x��
x��
S��AEF��y��![]() ��
��
��ͼB����AD��x��AB����![]() ��x��5ʱ��
��x��5ʱ��
��EF��AB��
��Rt��BEF��Rt��BCA��
��![]() ��
��
��AE��x����AEF�����Ϊy��![]() ��
��
��EF��![]() ��
��
![]() ��
��
������ͼA����0��x��AD����0��x��![]() ʱ��
ʱ��
![]() ��
��
��x��AD����x��![]() ʱ��y�����
ʱ��y�����![]() ��
��
��ͼB����AD��x��BD����![]() ��x��5ʱ��
��x��5ʱ��
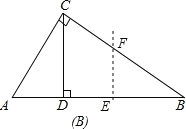
![]() ��y�����
��y�����![]() ����ʱx��2.5��5���ʳ�����
����ʱx��2.5��5���ʳ�����
��y�����![]() ��
��
��3�����ڣ�
������ڣ���0��x��5ʱ��
�ߡ�ABC���ܳ�Ϊ3+4+5��12��
��AE+AF��6��
��AF��6��x����0��6��x��3��
��3��x��6��
��3��x��5��
��FG��AB�ڵ�G��
�ɡ�AFG�ס�ACD��
��![]() ��
��
��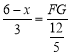 ��
��
��FG��![]() ��6��x����
��6��x����
��S��AEF��![]() ��
��
��3��![]() ��
��
��ã�x1��![]() ��x2��
��x2��![]() ��
��
��3��x��5��
��x1��![]() ���������⣩��x2��
���������⣩��x2��![]() ���������⣬��ȥ����
���������⣬��ȥ����
�ʴ���x��ֱ��EF����ABC���ܳ������ͬʱƽ�֣���ʱx��![]() ��
��

 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�����Ŀ�� ƶ���������ھ���ƶ�����ӵİ���£���һƬ��������ֲ������ˮ����ݮ�������㣬��ֲ�ɱ�Ϊ18Ԫ/ǧ�ˣ�������ʽ�������ۣ�ͨ��30����������֣���1������20ǧ�ˣ��Ժ�ÿ���ǰһ�����4ǧ�ˣ����ۼ۸�![]() Ԫ/ǧ�ˣ���ʱ��x���죩֮���������±���
Ԫ/ǧ�ˣ���ʱ��x���죩֮���������±���
ʱ�� | (1��x��20�� | (20��x��30�� |
���ۼ۸�y��Ԫ/ǧ�ˣ� | -0.5x+38 | 25 |
�����У�x��y��Ϊ������
��1��������������P��ǧ�ˣ���ʱ��![]() ���죩֮��ĺ�����ϵʽΪ ��
���죩֮��ĺ�����ϵʽΪ ��
��2����������ݮ�ڼ���ʱ�����������w�����������Ƕ���Ԫ��
��3����������30���У���������w������870Ԫ���������м��죮