题目内容
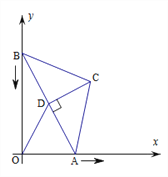
【题目】如图,在△ABC中,BC=AC=5,AB=8,CD为AB边的高,点A在x轴上,点B在y轴上,点C在第一象限,若A从原点出发,沿x轴向右以每秒1个单位长的速度运动,则点B随之沿y轴下滑,并带动△ABC在平面内滑动,设运动时间为t秒,当B到达原点时停止运动
(1)连接OC,线段OC的长随t的变化而变化,当OC最大时,t=____;
(2)当△ABC的边与坐标轴平行时,t=____。
【答案】 ![]() t=
t=![]()
【解析】试题解析:![]() 如图:
如图:
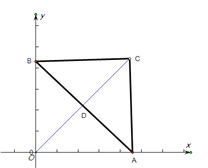
当![]() 三点共线时,
三点共线时,![]() 取得最大值,
取得最大值,![]()
![]()
![]()
![]() 分两种情况进行讨论:①设
分两种情况进行讨论:①设![]() 时,CA⊥OA,
时,CA⊥OA,
∴CA∥y轴,
∴∠CAD=∠ABO.
又![]()
∴Rt△CAD∽Rt△ABO,
∴![]() 即
即![]()
解得![]()
②设![]() 时,
时,![]()
∴CB∥x轴,
Rt△BCD∽Rt△ABO,
∴![]() 即
即![]()
![]()
综上可知,当以点C为圆心,CA为半径的圆与坐标轴相切时,t的值为![]() 或
或![]()
故答案为:![]()
![]()
![]() 或
或![]()

练习册系列答案
相关题目