题目内容
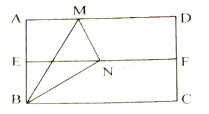
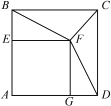
【题目】如图,正方形AEFG的顶点E、G在正方形ABCD的边AB、AD上,连接BF、DF.
![]() (1)求证:BF=DF;
(1)求证:BF=DF;
(2)连接CF,请直接写出![]() 的值为__________(不必写出计算过程).
的值为__________(不必写出计算过程).
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据正方形的性质得出BE=DG,再利用△BEF≌△DGF求得BF=DF,
(2)由BF=DF得点F在对角线AC上,再运用平行线间线段的比求解.
(1)∵四边形ABCD和AEFG都是正方形,
∴AB=AD,AE=AG=EF=FG,∠BEF=∠DGF=90°,
∴BE=AB-AE,DG=AD-AG,
∴BE=DG,
∴△BEF≌△DGF(SAS),
∴BF=DF;
(2)连接AC,
∵BF=DF
∴点F在对角线AC上,
∵AD∥EF∥BC,
∴CF:BE=AF:AE=![]() AE:AE=
AE:AE=![]() ,
,
∴CF:BE=![]() .
.


练习册系列答案
相关题目
【题目】某校开展“文明在行动”的志愿者活动,准备购买某一品牌书包送到希望学校.在![]() 商店,无论一次购买多少,价格均为每个50元.在
商店,无论一次购买多少,价格均为每个50元.在![]() 商店,一次购买数量不超过10个时,价格为每个60元;一次购买数量超过10个时,超出10个部分打八折.设一次购买该品牌书包的数量为x个.
商店,一次购买数量不超过10个时,价格为每个60元;一次购买数量超过10个时,超出10个部分打八折.设一次购买该品牌书包的数量为x个.
(Ⅰ)根据题意填表:
一次购买数量/个 | 5 | 10 | 15 | … |
| 500 | … | ||
| 600 | … |
(Ⅱ)设在![]() 商店花费
商店花费![]() 元,在
元,在![]() 商店花费
商店花费![]() 元,分别求出
元,分别求出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(Ⅲ)根据题意填空;
①若小丽在![]() 商店和在
商店和在![]() 商店一次购买书包的数量相同,且花费相同,则她在同一商店一次购买书包的数量为______个.
商店一次购买书包的数量相同,且花费相同,则她在同一商店一次购买书包的数量为______个.
②若小丽在同一商店一次购买书包的数量为50个,则她在![]() 两个商店中的______商店购买花费少;
两个商店中的______商店购买花费少;
③若小丽在同一商店一次购买书包花费了1800元,则她在![]() 两个商店中_______商店购买数量多.
两个商店中_______商店购买数量多.