题目内容
已知,如图,MN⊥AB,垂足为G,MN⊥CD,垂足为H,直线EF分别交AB、CD于G、Q,∠GQC=120°,求∠EGB和∠HGQ的度数。

【答案】
∠EGB=60°,∠HGQ=30°
【解析】
试题分析:由MN⊥AB,MN⊥CD可得AB∥CD,根据平行线的性质可得∠EGB=∠EQH,再结合∠GQC=120°即可求得∠EGB和∠HGQ的度数。
∵MN⊥AB,MN⊥CD
∴∠MGB=∠MHD=90°
∴AB∥CD
∴∠EGB=∠EQH
∵∠EQH=180°-∠GQC=180°-120°=60°
∴∠EGB=60°
∴∠EGM=90°-∠EGB=30°
∴∠EGB=60°,∠HGQ=30°.
考点:本题考查的是平行线的判定和性质
点评:解答本题的关键是熟练掌握垂直于同一条直线的两条直线互相平行;两直线平行,同位角相等.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
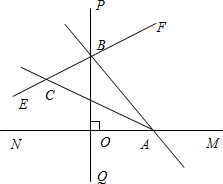 PBA与∠BAO的平分线相交于点C.
PBA与∠BAO的平分线相交于点C.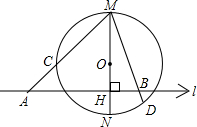 已知:如图,MN为⊙O的直径,l⊥MN于H,割线MCA及弦MBD分别交⊙O于C、D.
已知:如图,MN为⊙O的直径,l⊥MN于H,割线MCA及弦MBD分别交⊙O于C、D. 25、已知,如图,MN是?ABCD外的一条直线,AA′、BB′、CC′、DD′都垂直于MN,A′、B′、C′、D′为垂足.求证:AA′+CC′=BB′+DD′.
25、已知,如图,MN是?ABCD外的一条直线,AA′、BB′、CC′、DD′都垂直于MN,A′、B′、C′、D′为垂足.求证:AA′+CC′=BB′+DD′. (1998•海淀区)已知:如图,MN是⊙O的切线,切点为A,MN平行于弦CD,弦AB交CD于点E.
(1998•海淀区)已知:如图,MN是⊙O的切线,切点为A,MN平行于弦CD,弦AB交CD于点E.