题目内容
已知:如图,MN⊥PQ,垂足为O,点A、B分别在射线上OM、OP上,直线BE平分∠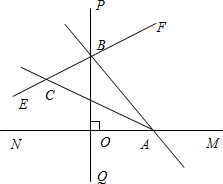 PBA与∠BAO的平分线相交于点C.
PBA与∠BAO的平分线相交于点C.(1)若∠BAO=45°,求∠ACB;
(2)若点A、B分别在射线上OM、OP上移动,试问∠ACB的大小是否会发生变化?如果保持不变,请说明理由;如果随点A、B的移动发生变化,请求出变化的范围.
分析:(1)根据三角形的一个外角等于与它不相邻的两个内角的和求出∠PBA,然后根据角平分线的定义表示出∠FBA与∠BAC,最后在△ABC中,利用三角形的外角性质即可求解;
(2)根据(1)的求解思路,求出∠ACB的表达式,是常数,所以不论点A、B如何移动,角的大小保持不变.
(2)根据(1)的求解思路,求出∠ACB的表达式,是常数,所以不论点A、B如何移动,角的大小保持不变.
解答:解:(1)∵MN⊥PQ,
∴∠BOA=90°,
在△ABO中,∠PBA=∠BAO+∠BOA=45°+90°=135°,
∵∠PBA与∠BAO的平分线相交于点C,
∴∠BAC=
∠BAO=
×45°=22.5°,
∠FBA=
∠PBA=
×135°=67.5°,
在△ABC中,∠ACB=∠FBA-∠BAC=67.5°-22.5°=45°;
(2)∵MN⊥PQ,
∴∠BOA=90°,
在△ABO中,∠PBA=∠BAO+∠BOA=∠BAO+90°,
∵∠PBA与∠BAO的平分线相交于点C,
∴∠BAC=
∠BAO,
∠FBA=
∠PBA=
(∠BAO+90°)=
∠BAO+45°,
在△ABC中,∠ACB=∠FBA-∠BAC=
∠BAO+45°-
∠BAO=45°.
∴∠BOA=90°,
在△ABO中,∠PBA=∠BAO+∠BOA=45°+90°=135°,
∵∠PBA与∠BAO的平分线相交于点C,
∴∠BAC=
| 1 |
| 2 |
| 1 |
| 2 |
∠FBA=
| 1 |
| 2 |
| 1 |
| 2 |
在△ABC中,∠ACB=∠FBA-∠BAC=67.5°-22.5°=45°;
(2)∵MN⊥PQ,
∴∠BOA=90°,
在△ABO中,∠PBA=∠BAO+∠BOA=∠BAO+90°,
∵∠PBA与∠BAO的平分线相交于点C,
∴∠BAC=
| 1 |
| 2 |
∠FBA=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
在△ABC中,∠ACB=∠FBA-∠BAC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了三角形的内角和定理,一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,求出各角的表达式是解题的关键,难度中等.

练习册系列答案
相关题目
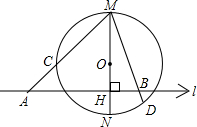 已知:如图,MN为⊙O的直径,l⊥MN于H,割线MCA及弦MBD分别交⊙O于C、D.
已知:如图,MN为⊙O的直径,l⊥MN于H,割线MCA及弦MBD分别交⊙O于C、D. 25、已知,如图,MN是?ABCD外的一条直线,AA′、BB′、CC′、DD′都垂直于MN,A′、B′、C′、D′为垂足.求证:AA′+CC′=BB′+DD′.
25、已知,如图,MN是?ABCD外的一条直线,AA′、BB′、CC′、DD′都垂直于MN,A′、B′、C′、D′为垂足.求证:AA′+CC′=BB′+DD′. (1998•海淀区)已知:如图,MN是⊙O的切线,切点为A,MN平行于弦CD,弦AB交CD于点E.
(1998•海淀区)已知:如图,MN是⊙O的切线,切点为A,MN平行于弦CD,弦AB交CD于点E.