Question

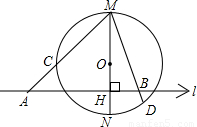
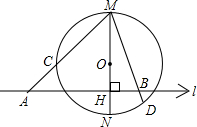已知：如图，MN为⊙O的直径，l⊥MN于H，割线MCA及弦MBD分别交⊙O于C、D．
求证：MA•MC=MB•MD．

Answer 1

分析：先连接CN、DN，有MN⊥l，AB是直径，可得一组对应角都是90°，再加上一对公共角，可证两个直角三角形全等Rt△MND∽Rt△MBH，由此可得比例线段，同理可证另一对直角三角形全等Rt△AHM∽Rt△NCM，也可得比例线段，利用等量代换，可证此题．

解答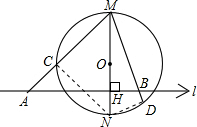：证明：连接CN、DN，（1分）
∵MN是直径，
∴∠D=90°（1分）
∵l⊥MN，
∴∠MHB=90°（1分）
在△MND与△MBH中，∵∠BMH=∠NMD，
∴Rt△MND∽Rt△MBH，
∴

MN

MB

=

MD

MH

∴MB•MD=MN•MH①（2分）
同理可证Rt△AHM∽Rt△NCM，
∴

MN

MA

=

MC

MH

．
∴MN•MH=MA•MC②（2分）
由①、②，有MA•MC=MB•MD．

点评：本题利用了直径所对的圆周角是90°、相似三角形的判定和性质、等量代换等知识．