题目内容
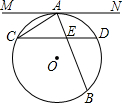（1998•海淀区）已知：如图，MN是⊙O的切线，切点为A，MN平行于弦CD，弦AB交CD于点E．求证：AC2=AE•AB．
分析：连接AO并延长交⊙O于点F，连接CF，CB，利用切线的性质和圆周角定理得到∠MAC=∠F后即可得到△ACE∽△ABC，从而证得结论．
解答：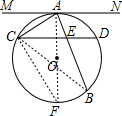
证明：连接AO并延长交⊙O于点F，连接CF，CB，
∵MN是⊙O的切线，
∴FA⊥MN，
∴∠MAC+∠CAF=90°，
∵AF过点O，
∴∠ACF=90°，
∴∠CAF+∠F=90°，
∴∠MAC=∠F
∵∠CAB=∠CAB
∴△ACE∽△ABC
∴
=
∴AC2=AE•AB．
证明：连接AO并延长交⊙O于点F，连接CF，CB，∵MN是⊙O的切线，
∴FA⊥MN，
∴∠MAC+∠CAF=90°，
∵AF过点O，
∴∠ACF=90°，
∴∠CAF+∠F=90°，
∴∠MAC=∠F
∵∠CAB=∠CAB
∴△ACE∽△ABC
∴
| AC |
| AB |
| AE |
| AC |
∴AC2=AE•AB．
点评：本题考查了切线的性质及相似三角形的判定与性质，解题的关键是正确的作出如图的辅助线．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目