题目内容
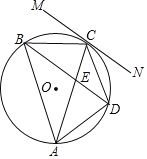
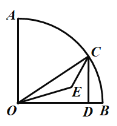
【题目】如图,扇形AOB,且OB=4,∠AOB=90°,C为弧AB上任意一点,过C点作CD⊥OB于点D,设△ODC的内心为E,连接OE、CE,当点C从点B运动到点A时,内心E所经过的路径长为 ________.
【答案】![]()
【解析】
根据题意先利用内心的性质求出∠OEC的度数和∠COE=∠BOE,易证△COE≌△BOE,利用全等三角形的性质得∠OEB=∠OEC=135°,从而确定出点E的运动轨迹,则劣弧OB的长即为所求.
解:∵CD⊥OB
∴∠ODC=90°
∵点E是△ODC的内心
∴∠OEC=90°+![]() ∠ODC=135°,∠COE=∠BOE
∠ODC=135°,∠COE=∠BOE
又∵OE=OE,OB=OC
∴△COE≌△BOE
∴∠OEB=∠OEC=135°
∴点E的运动轨迹为:以OB为弦,并且弦OB所对圆周角为135°的一段劣弧.
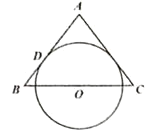
设经过点O、B、E三点的圆M如图所示,
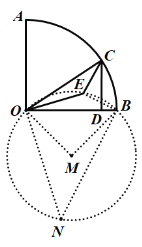
则∠N=180°-∠OEB=45°
∴∠M=2∠N=90°
∴OM=BM=![]() OB=2
OB=2![]()
∴劣弧OB的长![]()
∴内心E所经过的路径长为![]() .
.
故答案为:![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目