题目内容
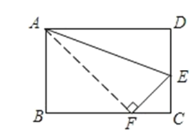
【题目】如图,二次函数![]() 的图像与x轴交于点A(-1,0)、B(3,0),与y轴交于点C(0,3).
的图像与x轴交于点A(-1,0)、B(3,0),与y轴交于点C(0,3).
(1)求二次函数的表达式;
(2)设上述抛物线的对称轴l与x轴交于点D,过点C作CE⊥l于E,P为线段DE上一点,Q(m,0)为x轴负半轴上一点,以P、Q、D为顶点的三角形与△CPE相似;
①当满足条件的![]() 点有且只有三个时,求
点有且只有三个时,求![]() 的取值范围;
的取值范围;
②若满足条件的![]() 点有且只有两个,直接写出
点有且只有两个,直接写出![]() 的值.
的值.

【答案】(1)y=-x2+2x+3;(2)![]() 且
且![]() ;(3)-1或-
;(3)-1或-![]() .
.
【解析】试题分析:(1)将二次函数解析式设为一般式,将三个点的坐标带入解析式,求出未知参数即可;(2)①设PD=x(0<x<3),则PE=3-x,以P、Q、D为顶点的三角形与△CPE相似一共有两种情况,△CPE∽△QPD以及△CPE∽△PQD,当△CPE∽△QPD时, ![]() ,即
,即![]() ,由此可得一个关于x的一元一次方程,根据m的范围分析得出方程有解;当△CPE∽△PQD,则
,由此可得一个关于x的一元一次方程,根据m的范围分析得出方程有解;当△CPE∽△PQD,则![]() ,即
,即![]() ,整理可得一个关于x的一元二次方程,由于满足条件的
,整理可得一个关于x的一元二次方程,由于满足条件的![]() 点有且只有三个,故此一元二次方程必有两个不相等的实数根,即b2-4ac>0,求出m的范围;此外还需考虑当1-m=x时,三解中有两解相同,将x=1-m代入
点有且只有三个,故此一元二次方程必有两个不相等的实数根,即b2-4ac>0,求出m的范围;此外还需考虑当1-m=x时,三解中有两解相同,将x=1-m代入![]() ,求出x,再求出对应的m不能取的数值;综上,写出m的范围;②由第①问直接写出m的取值即可.
,求出x,再求出对应的m不能取的数值;综上,写出m的范围;②由第①问直接写出m的取值即可.
试题解析:
解:(1)将A(-1,0)、B(3,0)、C(0,3)代入y=ax2+bx+c中,得:
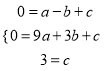 ,解得
,解得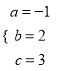 ,
,
∴二次函数的表达式为y=-x2+2x+3;
(2)①抛物线对称轴为x=1,
设PD=x(0<x<3),则PE=3-x.
若△CPE∽△QPD,则![]() ,即
,即![]() ,
,
整理得:(2-m)x=3-3m,
∵m<0,∴x=![]() =3-
=3-![]() ≠0是方程的根;
≠0是方程的根;
若△CPE∽△PQD,则![]() ,即
,即![]() ,
,
即x2-3x+1-m=0,
由题意得:b2-4ac>0,即(-3)2-4(1-m)>0,解得m>-![]() ,
,
当1-m=x时,三解中有两解相同,将x=1-m代入![]() ,
,
解得x1=0(舍),x2=2,
代入得m=-1,故排除m=-1.
所以m的范围是-![]() <m<0,且m≠-1.
<m<0,且m≠-1.
②m的值为-1或-![]() .
.

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案【题目】(1)下表是2008年北京奥运会部分国家金牌榜:
国家 | 中国 | 美国 | 俄罗斯 | 英国 | 德国 | 澳大利亚 | 本届奥运会金牌总数 |
金牌数 | 51 | 36 | 23 | 19 | 16 | 14 | 302 |
①选择 统计图来描述上表中各国金牌数最恰当.请把这个统计图画出来.
②请你根据统计图,写出两条与29届奥运会金牌数有关的信息.
(2)下表是中国奥运代表团自1984年第23届洛杉矶奥运会以来,历届奥运会的金牌总数统计表:
年份 | 1984 | 1988 | 1992 | 1996 | 2000 | 2004 | 2008 |
届别 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
金牌数 | 15 | 5 | 16 | 16 | 28 | 32 | 51 |
①选择 统计图来描述上表中我国各届金牌数最恰当.把这个统计图画出来.
②请你根据统计图,写出两条与中国奥运金牌数相关的信息.