题目内容
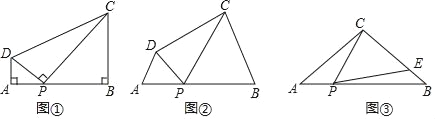
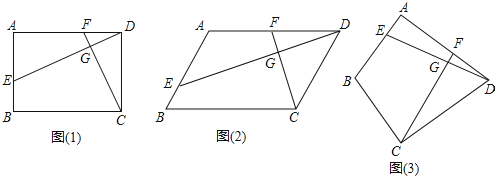
【题目】已知四边形ABCD中,E,F分别是AB,AD边上的点,DE与CF交于点G.
(1)如图1,若四边形ABCD是矩形,且DE⊥CF.证明:![]() =
=![]() ;
;
(2)如图2,若四边形ABCD是平行四边形,试探究:
当∠B与∠EGC满足什么关系时,使得![]() =
=![]() 成立?并证明你的结论;
成立?并证明你的结论;
(3)如图3,若BA=BC= 3,DA=DC= 4,∠BAD= 90°,DE⊥CF.求![]() 的值.
的值.
【答案】(1)见解析;(2)当∠B+∠EGC=180°时,![]() =
=![]() 成立.证明见解析;(3)
成立.证明见解析;(3)![]() .
.
理由见解析.
【解析】
(1)根据矩形性质得出∠A=∠FDC=90°,求出∠CFD=∠AED,证出△AED∽△DFC即可;
(2)当∠B+∠EGC=180°时,DECD=CFAD成立,证△DFG∽△DEA,得出![]() ,证△CGD∽△CDF,得出
,证△CGD∽△CDF,得出![]() ,即可得出答案;
,即可得出答案;
(3)过C作CN⊥AD于N,CM⊥AB交AB延长线于M,连接BD,设CN=x,△BAD≌△BCD,推出∠BCD=∠A=90°,证△BCM∽△DCN,求出CM=![]() x,在Rt△CMB中,由勾股定理得出BM2+CM2=BC2,代入得出方程(x-3)2+(
x,在Rt△CMB中,由勾股定理得出BM2+CM2=BC2,代入得出方程(x-3)2+(![]() x)2=62,求出CN=
x)2=62,求出CN=![]() ,证出△AED∽△NFC,即可得出答案.
,证出△AED∽△NFC,即可得出答案.
(1)证明:∵四边形ABCD是矩形,
∴∠A=∠FDC=90°,
∵CF⊥DE,
∴∠DGF=90°,
∴∠ADE+∠CFD=90°,∠ADE+∠AED=90°,
∴∠CFD=∠AED,
∵∠A=∠CDF,
∴△AED∽△DFC,
∴![]() ,即
,即![]() =
=![]() .
.
(2)当∠B+∠EGC=180°时,![]() =
=![]() 成立.
成立.
证明:∵四边形ABCD是平行四边形,
∴∠B=∠ADC,AD∥BC,
∴∠B+∠A=180°,
∵∠B+∠EGC=180°,
∴∠A=∠EGC=∠FGD,
∵∠FDG=∠EDA,
∴△DFG∽△DEA,
∴![]() ,
,
∵∠B=∠ADC,∠B+∠EGC=180°,∠EGC+∠DGC=180°,
∴∠CGD=∠CDF,
∵∠GCD=∠DCF,
∴△CGD∽△CDF,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即当∠B+∠EGC=180°时,![]() 成立.
成立.
(3)解:![]() .
.
理由是:过C作CN⊥AD于N,CM⊥AB交AB延长线于M,连接BD,
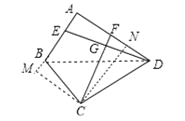
设CN=x,
∵AB⊥AD,
∴∠A=∠M=∠CNA=90°,
∴四边形AMCN是矩形,
∴AM=CN,AN=CM,
∵在△BAD和△BCD中
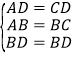
∴△BAD≌△BCD(SSS),
∴∠BCD=∠A=90°,
∴∠ABC+∠ADC=180°,
∵∠ABC+∠CBM=180°,
∴∠CBM=∠ADC,
∵∠CND=∠M=90°,
∴△BCM∽△DCN,
∴![]() ,
,
∴![]()
∴![]()
在Rt△CMB中,![]() ,BM=AM﹣AB=x﹣3,由勾股定理得:
,BM=AM﹣AB=x﹣3,由勾股定理得:![]() ,
,
∴![]() ,
,
解得x=0(舍去),x=![]()
∴CN=![]() ,
,
∵∠A=∠FGD=90°,
∴∠AED+∠AFG=180°,
∵∠AFG+∠NFC=180°,
∴∠AED=∠CFN,
∵∠A=∠CNF=90°,
∴△AED∽△NFC,
∴![]()

 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案