题目内容
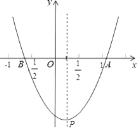
【题目】已知:抛物线y=-![]() +bx+c经过A(-1,0)、B(5,0)两点,顶点为P.
+bx+c经过A(-1,0)、B(5,0)两点,顶点为P.
求:(1)求b,c的值;
(2)求△ABP的面积;
(3)若点C(![]() ,
,![]() )和点D(
)和点D(![]() ,
,![]() )在该抛物线上,则当
)在该抛物线上,则当![]() 时,请写出
时,请写出![]() 与
与![]() 的大小关系.
的大小关系.
【答案】(1)b=4,c=5;(2)27;(3)y1<y2.
【解析】
(1)利用交点式得到y=-(x+1)(x-5),然后展开即可得到b和c的值;
(2)先把抛物线的解析式配成顶点式得到P点坐标为(2,9),然后根据三角形面积公式计算即可;
(3)由于抛物线的对称轴为直线x=2,开口向下,则根据二次函数的性质可确定y1与y2的大小关系.
(1)把点A(-1, 0)、B(5,0)分别代入y=-![]() +bx+c, 得
+bx+c, 得![]() ,
,
解得![]() .
.
(2)由(1)得抛物线解析式y=-![]() +4x+5
+4x+5
∴y=-(x-2)2-9
∴P(2,9)
∵A(-1, 0)、B(5,0)
∴AB=6
∴S△ABF=![]() .
.
(3)∵抛物线开口向下
∴在对称轴直线x=2的左侧y随着x的增大而增大
∴![]() <
<![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目