题目内容
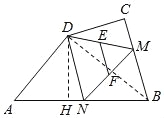
【题目】如图,四边形ABCD中,∠A=60°,AD=2,AB=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
试题分析:根据三角形的中位线定理得出EF=![]() DN,从而可知DN最大时,EF最大,因为N与B重合时DN最大,此时根据勾股定理求得DN,从而求得EF的最大值. 连接DB,过点D作DH⊥AB交AB于点H,
DN,从而可知DN最大时,EF最大,因为N与B重合时DN最大,此时根据勾股定理求得DN,从而求得EF的最大值. 连接DB,过点D作DH⊥AB交AB于点H,
∵ED=EM,MF=FN, ∴EF=![]() DN, ∴DN最大时,EF最大, ∴N与B重合时DN=DB最大,
DN, ∴DN最大时,EF最大, ∴N与B重合时DN=DB最大,
在Rt△ADH中, ∵∠A=60° ∴DH=ADsin60°=2×![]() =
=![]() ,AH=ADcos60°=2×
,AH=ADcos60°=2×![]() =1,
=1,
∴BH=AB﹣AH=3﹣1=2, ∴DB=![]() =
=![]() =
=![]() , ∴EFmax=
, ∴EFmax=![]() DB=
DB=![]() , ∴EF的最大值为
, ∴EF的最大值为![]() .
.

练习册系列答案
相关题目