题目内容
【题目】如图,PA、PB是⊙O的切线,A,B为切点,∠OAB=30度.
(1)求∠APB的度数;
(2)当OA=3时,求AP的长.
【答案】
(1)解:∵在△ABO中,OA=OB,∠OAB=30°,
∴∠AOB=180°﹣2×30°=120°,
∵PA、PB是⊙O的切线,
∴OA⊥PA,OB⊥PB,即∠OAP=∠OBP=90°,
∴在四边形OAPB中,
∠APB=360°﹣120°﹣90°﹣90°=60°
∵PA、PB是⊙O的切线∴PA=PB,OA⊥PA;
∵∠OAB=30°,OA⊥PA,
∴∠BAP=90°﹣30°=60°,
∴△ABP是等边三角形,
∴∠APB=60°.
(2)解:如图①,连接OP;
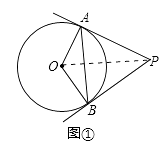
∵PA、PB是⊙O的切线,
∴PO平分∠APB,即∠APO= ![]() ∠APB=30°,
∠APB=30°,
又∵在Rt△OAP中,OA=3,∠APO=30°,
∴AP= ![]() =3
=3 ![]() .
.
方法二:如图②,作OD⊥AB交AB于点D;
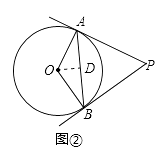
∵在△OAB中,OA=OB,
∴AD= ![]() AB;
AB;
∵在Rt△AOD中,OA=3,∠OAD=30°,
∴AD=OAcos30°= ![]() ,
,
∴AP=AB= ![]() .
.
【解析】(1)根据等腰三角形的性质,求出∠AOB的度数,根据切线的性质和四边形内角和,求出∠APB的度数;(2)根据垂径定理,得到AD与AB的关系,在Rt△AOD中,根据特殊角的函数值求出AP=AB.

 阅读快车系列答案
阅读快车系列答案【题目】某工厂设门市部专卖某产品,该每件成本每件成本30元,从开业一段时间的每天销售统计中,随机抽取一部分情况如下表所示:
销售单位(元) | 50 | 60 | 70 | 75 | 80 | 85 | … |
日销售量 | 300 | 240 | 180 | 150 | 120 | 90 | … |
假设每天定的销价是不变的,且每天销售情况均服从这种规律.
(1)秋日销售量与销售价格之间满足的函数关系式;
(2)门市部原设定两名销售员,担当销售量较大时,在每天售出量超过198件时,则必须增派一名营业员才能保证营业有序进行.设营业员每人每天工资为40元,求每件产品应定价多少元,才能使每天门市部纯利润最大?(纯利润=总销售﹣成本﹣营业员工资)





