题目内容
设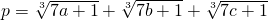
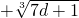 .其中a,b,c,d是正实数,且满足a+b+c+d=1.则p满足
.其中a,b,c,d是正实数,且满足a+b+c+d=1.则p满足
- A.p>5
- B.p<5
- C.p<2
- D.p<3
A
分析:先根据已知条件确定出a、b、c、d的取值范围,根据不等式的基本性质得出a>a2>a3,再比较出有 >a+1,同理即可得出理
>a+1,同理即可得出理 >b+1,
>b+1, >c+1,
>c+1,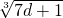 >d+1,最后把四式相加即可得出结论.
>d+1,最后把四式相加即可得出结论.
解答:∵a,b,c,d是正实数,且满足a+b+c+d=1,
∴0<a<1,
∴a>a2>a3,
∴7a+1>(a+1)3,有 >a+1,
>a+1,
同理 >b+1,
>b+1, >c+1,
>c+1,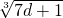 >d+1,
>d+1,
∴p>(a+b+c+d)+4=5.
故选A.
点评:本题考查的是实数的概念、不等式的基本性质,能根据不等式的基本性质得出 >a+1是解答此题的关键.
>a+1是解答此题的关键.
分析:先根据已知条件确定出a、b、c、d的取值范围,根据不等式的基本性质得出a>a2>a3,再比较出有
 >a+1,同理即可得出理
>a+1,同理即可得出理 >b+1,
>b+1, >c+1,
>c+1,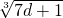 >d+1,最后把四式相加即可得出结论.
>d+1,最后把四式相加即可得出结论.解答:∵a,b,c,d是正实数,且满足a+b+c+d=1,
∴0<a<1,
∴a>a2>a3,
∴7a+1>(a+1)3,有
 >a+1,
>a+1,同理
 >b+1,
>b+1, >c+1,
>c+1,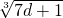 >d+1,
>d+1,∴p>(a+b+c+d)+4=5.
故选A.
点评:本题考查的是实数的概念、不等式的基本性质,能根据不等式的基本性质得出
 >a+1是解答此题的关键.
>a+1是解答此题的关键. 
练习册系列答案
相关题目
 ,其中
,其中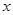 可取
可取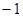 、2,
、2,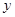 可取
可取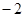 、3.
、3.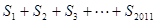 = ▲
= ▲ 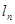 :
: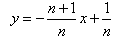 (n是不为零的自然数).当
(n是不为零的自然数).当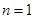 时,直线
时,直线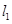 :
: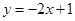 与x轴和y轴分别交于点
与x轴和y轴分别交于点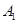 和
和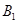 ,设△
,设△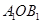 (其中O是平面直角坐标系的原点)的面积为
(其中O是平面直角坐标系的原点)的面积为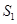 ;当
;当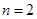 时,直线
时,直线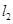 :
: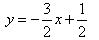 与x轴和y轴分别交于点
与x轴和y轴分别交于点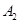 和
和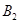 ,设△
,设△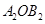 的面积为
的面积为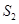 ;…依此类推,直线
;…依此类推,直线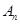 和
和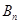 ,设△
,设△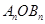 的面积为
的面积为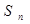 .则
.则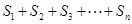 =________,
=________,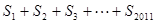 = ▲
= ▲